| VK Cup 2016 - Round 3 |
|---|
| Finished |
One social network developer recently suggested a new algorithm of choosing ads for users.
There are n slots which advertisers can buy. It is possible to buy a segment of consecutive slots at once. The more slots you own, the bigger are the chances your ad will be shown to users.
Every time it is needed to choose ads to show, some segment of slots is picked by a secret algorithm. Then some advertisers are chosen. The only restriction is that it should be guaranteed for advertisers which own at least p% of slots composing this segment that their ad will be shown.
From the other side, users don't like ads. So it was decided to show no more than 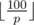 ads at once. You are asked to develop a system to sell segments of slots and choose ads in accordance with the rules described above.
ads at once. You are asked to develop a system to sell segments of slots and choose ads in accordance with the rules described above.
The first line of the input contains three integers n, m and p (1 ≤ n, m ≤ 150 000, 20 ≤ p ≤ 100) — the number of slots, the number of queries to your system and threshold for which display of the ad is guaranteed.
Next line contains n integers ai (1 ≤ ai ≤ 150 000), where the i-th number means id of advertiser who currently owns the i-th slot.
Next m lines contain queries descriptions. Each description is of one of the following forms:
- 1 l r id (1 ≤ l ≤ r ≤ n, 1 ≤ id ≤ 150 000) — advertiser id bought all slots in a range from l to r inclusive;
- 2 l r (1 ≤ l ≤ r) — you need to choose advertisers for segment [l, r].
For each query of the second type answer should be printed in a separate line. First integer of the answer should be the number of advertisements that will be shown 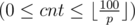 . Next cnt integers should be advertisers' ids.
. Next cnt integers should be advertisers' ids.
It is allowed to print one advertiser more than once, but each advertiser that owns at least 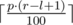 slots of the segment from l to r should be in your answer.
slots of the segment from l to r should be in your answer.
5 9 33
1 2 1 3 3
2 1 5
2 1 5
2 1 3
2 3 3
1 2 4 5
2 1 5
2 3 5
1 4 5 1
2 1 5
3 1 2 3
2 1 3
2 2 1
3 1 1000 1000
1 5
2 5 3
2 1 5
Samples demonstrate that you actually have quite a lot of freedom in choosing advertisers.
| Name |
|---|




