A tree is a connected undirected graph consisting of n vertices and n - 1 edges. Vertices are numbered 1 through n.
Limak is a little polar bear. He once had a tree with n vertices but he lost it. He still remembers something about the lost tree though.
You are given m pairs of vertices (a1, b1), (a2, b2), ..., (am, bm). Limak remembers that for each i there was no edge between ai and bi. He also remembers that vertex 1 was incident to exactly k edges (its degree was equal to k).
Is it possible that Limak remembers everything correctly? Check whether there exists a tree satisfying the given conditions.
The first line of the input contains three integers n, m and k (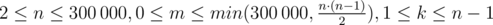 ) — the number of vertices in Limak's tree, the number of forbidden pairs of vertices, and the degree of vertex 1, respectively.
) — the number of vertices in Limak's tree, the number of forbidden pairs of vertices, and the degree of vertex 1, respectively.
The i-th of next m lines contains two distinct integers ai and bi (1 ≤ ai, bi ≤ n, ai ≠ bi) — the i-th pair that is forbidden. It's guaranteed that each pair of vertices will appear at most once in the input.
Print "possible" (without quotes) if there exists at least one tree satisfying the given conditions. Otherwise, print "impossible" (without quotes).
5 4 2
1 2
2 3
4 2
4 1
possible
6 5 3
1 2
1 3
1 4
1 5
1 6
impossible
In the first sample, there are n = 5 vertices. The degree of vertex 1 should be k = 2. All conditions are satisfied for a tree with edges 1 - 5, 5 - 2, 1 - 3 and 3 - 4.
In the second sample, Limak remembers that none of the following edges existed: 1 - 2, 1 - 3, 1 - 4, 1 - 5 and 1 - 6. Hence, vertex 1 couldn't be connected to any other vertex and it implies that there is no suitable tree.
| Name |
|---|




