| Codeforces Round 356 (Div. 1) |
|---|
| Finished |
Limak, a bear, isn't good at handling queries. So, he asks you to do it.
We say that powers of 42 (numbers 1, 42, 1764, ...) are bad. Other numbers are good.
You are given a sequence of n good integers t1, t2, ..., tn. Your task is to handle q queries of three types:
- 1 i — print ti in a separate line.
- 2 a b x — for
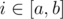 set ti to x. It's guaranteed that x is a good number.
set ti to x. It's guaranteed that x is a good number. - 3 a b x — for
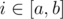 increase ti by x. After this repeat the process while at least one ti is bad.
increase ti by x. After this repeat the process while at least one ti is bad.
You can note that after each query all ti are good.
The first line of the input contains two integers n and q (1 ≤ n, q ≤ 100 000) — the size of Limak's sequence and the number of queries, respectively.
The second line of the input contains n integers t1, t2, ..., tn (2 ≤ ti ≤ 109) — initial elements of Limak's sequence. All ti are good.
Then, q lines follow. The i-th of them describes the i-th query. The first number in the line is an integer typei (1 ≤ typei ≤ 3) — the type of the query. There is at least one query of the first type, so the output won't be empty.
In queries of the second and the third type there is 1 ≤ a ≤ b ≤ n.
In queries of the second type an integer x (2 ≤ x ≤ 109) is guaranteed to be good.
In queries of the third type an integer x (1 ≤ x ≤ 109) may be bad.
For each query of the first type, print the answer in a separate line.
6 12
40 1700 7 1672 4 1722
3 2 4 42
1 2
1 3
3 2 6 50
1 2
1 4
1 6
2 3 4 41
3 1 5 1
1 1
1 3
1 5
1742
49
1842
1814
1822
43
44
107
After a query 3 2 4 42 the sequence is 40, 1742, 49, 1714, 4, 1722.
After a query 3 2 6 50 the sequence is 40, 1842, 149, 1814, 104, 1822.
After a query 2 3 4 41 the sequence is 40, 1842, 41, 41, 104, 1822.
After a query 3 1 5 1 the sequence is 43, 1845, 44, 44, 107, 1822.
| Name |
|---|




