| Educational Codeforces Round 14 |
|---|
| Finished |
You are given n integers a1, a2, ..., an.
A sequence of integers x1, x2, ..., xk is called a "xor-sequence" if for every 1 ≤ i ≤ k - 1 the number of ones in the binary representation of the number xi  xi + 1's is a multiple of 3 and
xi + 1's is a multiple of 3 and 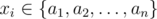 for all 1 ≤ i ≤ k. The symbol
for all 1 ≤ i ≤ k. The symbol  is used for the binary exclusive or operation.
is used for the binary exclusive or operation.
How many "xor-sequences" of length k exist? Output the answer modulo 109 + 7.
Note if a = [1, 1] and k = 1 then the answer is 2, because you should consider the ones from a as different.
The first line contains two integers n and k (1 ≤ n ≤ 100, 1 ≤ k ≤ 1018) — the number of given integers and the length of the "xor-sequences".
The second line contains n integers ai (0 ≤ ai ≤ 1018).
Print the only integer c — the number of "xor-sequences" of length k modulo 109 + 7.
5 2
15 1 2 4 8
13
5 1
15 1 2 4 8
5
| Name |
|---|




