| Codeforces Round 370 (Div. 2) |
|---|
| Finished |
There are n casinos lined in a row. If Memory plays at casino i, he has probability pi to win and move to the casino on the right (i + 1) or exit the row (if i = n), and a probability 1 - pi to lose and move to the casino on the left (i - 1) or also exit the row (if i = 1).
We say that Memory dominates on the interval i... j if he completes a walk such that,
- He starts on casino i.
- He never looses in casino i.
- He finishes his walk by winning in casino j.
Note that Memory can still walk left of the 1-st casino and right of the casino n and that always finishes the process.
Now Memory has some requests, in one of the following forms:
- 1 i a b: Set
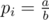 .
. - 2 l r: Print the probability that Memory will dominate on the interval l... r, i.e. compute the probability that Memory will first leave the segment l... r after winning at casino r, if she starts in casino l.
It is guaranteed that at any moment of time p is a non-decreasing sequence, i.e. pi ≤ pi + 1 for all i from 1 to n - 1.
Please help Memory by answering all his requests!
The first line of the input contains two integers n and q(1 ≤ n, q ≤ 100 000), — number of casinos and number of requests respectively.
The next n lines each contain integers ai and bi (1 ≤ ai < bi ≤ 109) — 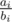 is the probability pi of winning in casino i.
is the probability pi of winning in casino i.
The next q lines each contain queries of one of the types specified above (1 ≤ a < b ≤ 109, 1 ≤ i ≤ n, 1 ≤ l ≤ r ≤ n).
It's guaranteed that there will be at least one query of type 2, i.e. the output will be non-empty. Additionally, it is guaranteed that p forms a non-decreasing sequence at all times.
Print a real number for every request of type 2 — the probability that boy will "dominate" on that interval. Your answer will be considered correct if its absolute error does not exceed 10 - 4.
Namely: let's assume that one of your answers is a, and the corresponding answer of the jury is b. The checker program will consider your answer correct if |a - b| ≤ 10 - 4.
3 13
1 3
1 2
2 3
2 1 1
2 1 2
2 1 3
2 2 2
2 2 3
2 3 3
1 2 2 3
2 1 1
2 1 2
2 1 3
2 2 2
2 2 3
2 3 3
0.3333333333
0.2000000000
0.1666666667
0.5000000000
0.4000000000
0.6666666667
0.3333333333
0.2500000000
0.2222222222
0.6666666667
0.5714285714
0.6666666667
| Name |
|---|




