The gym leaders were fascinated by the evolutions which took place at Felicity camp. So, they were curious to know about the secret behind evolving Pokemon.
The organizers of the camp gave the gym leaders a PokeBlock, a sequence of n ingredients. Each ingredient can be of type 0 or 1. Now the organizers told the gym leaders that to evolve a Pokemon of type k (k ≥ 2), they need to make a valid set of k cuts on the PokeBlock to get smaller blocks.
Suppose the given PokeBlock sequence is b0b1b2... bn - 1. You have a choice of making cuts at n + 1 places, i.e., Before b0, between b0 and b1, between b1 and b2, ..., between bn - 2 and bn - 1, and after bn - 1.
The n + 1 choices of making cuts are as follows (where a | denotes a possible cut):
Consider a sequence of k cuts. Now each pair of consecutive cuts will contain a binary string between them, formed from the ingredient types. The ingredients before the first cut and after the last cut are wasted, which is to say they are not considered. So there will be exactly k - 1 such binary substrings. Every substring can be read as a binary number. Let m be the maximum number out of the obtained numbers. If all the obtained numbers are positive and the set of the obtained numbers contains all integers from 1 to m, then this set of cuts is said to be a valid set of cuts.
For example, suppose the given PokeBlock sequence is 101101001110 and we made 5 cuts in the following way:
So the 4 binary substrings obtained are: 11, 010, 01 and 1, which correspond to the numbers 3, 2, 1 and 1 respectively. Here m = 3, as it is the maximum value among the obtained numbers. And all the obtained numbers are positive and we have obtained all integers from 1 to m. Hence this set of cuts is a valid set of 5 cuts.
A Pokemon of type k will evolve only if the PokeBlock is cut using a valid set of k cuts. There can be many valid sets of the same size. Two valid sets of k cuts are considered different if there is a cut in one set which is not there in the other set.
Let f(k) denote the number of valid sets of k cuts. Find the value of 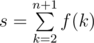 . Since the value of s can be very large, output s modulo 109 + 7.
. Since the value of s can be very large, output s modulo 109 + 7.
The input consists of two lines. The first line consists an integer n (1 ≤ n ≤ 75) — the length of the PokeBlock. The next line contains the PokeBlock, a binary string of length n.
Output a single integer, containing the answer to the problem, i.e., the value of s modulo 109 + 7.
4
1011
10
2
10
1
In the first sample, the sets of valid cuts are:
Size 2: |1|011, 1|01|1, 10|1|1, 101|1|.
Size 3: |1|01|1, |10|1|1, 10|1|1|, 1|01|1|.
Size 4: |10|1|1|, |1|01|1|.
Hence, f(2) = 4, f(3) = 4 and f(4) = 2. So, the value of s = 10.
In the second sample, the set of valid cuts is:
Size 2: |1|0.
Hence, f(2) = 1 and f(3) = 0. So, the value of s = 1.
| Name |
|---|




