| Codeforces Round 392 (Div. 2) |
|---|
| Finished |
For given n, l and r find the number of distinct geometrical progression, each of which contains n distinct integers not less than l and not greater than r. In other words, for each progression the following must hold: l ≤ ai ≤ r and ai ≠ aj , where a1, a2, ..., an is the geometrical progression, 1 ≤ i, j ≤ n and i ≠ j.
Geometrical progression is a sequence of numbers a1, a2, ..., an where each term after first is found by multiplying the previous one by a fixed non-zero number d called the common ratio. Note that in our task d may be non-integer. For example in progression 4, 6, 9, common ratio is 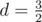 .
.
Two progressions a1, a2, ..., an and b1, b2, ..., bn are considered different, if there is such i (1 ≤ i ≤ n) that ai ≠ bi.
The first and the only line cotains three integers n, l and r (1 ≤ n ≤ 107, 1 ≤ l ≤ r ≤ 107).
Print the integer K — is the answer to the problem.
1 1 10
10
2 6 9
12
3 1 10
8
3 3 10
2
These are possible progressions for the first test of examples:
- 1;
- 2;
- 3;
- 4;
- 5;
- 6;
- 7;
- 8;
- 9;
- 10.
These are possible progressions for the second test of examples:
- 6, 7;
- 6, 8;
- 6, 9;
- 7, 6;
- 7, 8;
- 7, 9;
- 8, 6;
- 8, 7;
- 8, 9;
- 9, 6;
- 9, 7;
- 9, 8.
These are possible progressions for the third test of examples:
- 1, 2, 4;
- 1, 3, 9;
- 2, 4, 8;
- 4, 2, 1;
- 4, 6, 9;
- 8, 4, 2;
- 9, 3, 1;
- 9, 6, 4.
These are possible progressions for the fourth test of examples:
- 4, 6, 9;
- 9, 6, 4.
| Name |
|---|




