Tarly has two different type of items, food boxes and wine barrels. There are f food boxes and w wine barrels. Tarly stores them in various stacks and each stack can consist of either food boxes or wine barrels but not both. The stacks are placed in a line such that no two stacks of food boxes are together and no two stacks of wine barrels are together.
The height of a stack is defined as the number of items in the stack. Two stacks are considered different if either their heights are different or one of them contains food and other contains wine.
Jon Snow doesn't like an arrangement if any stack of wine barrels has height less than or equal to h. What is the probability that Jon Snow will like the arrangement if all arrangement are equiprobably?
Two arrangement of stacks are considered different if exists such i, that i-th stack of one arrangement is different from the i-th stack of the other arrangement.
The first line of input contains three integers f, w, h (0 ≤ f, w, h ≤ 105) — number of food boxes, number of wine barrels and h is as described above. It is guaranteed that he has at least one food box or at least one wine barrel.
Output the probability that Jon Snow will like the arrangement. The probability is of the form  , then you need to output a single integer p·q - 1 mod (109 + 7).
, then you need to output a single integer p·q - 1 mod (109 + 7).
1 1 1
0
1 2 1
666666672
In the first example f = 1, w = 1 and h = 1, there are only two possible arrangement of stacks and Jon Snow doesn't like any of them.
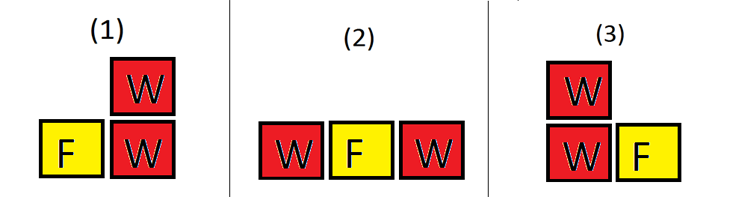
In the second example f = 1, w = 2 and h = 1, there are three arrangements. Jon Snow likes the (1) and (3) arrangement. So the probabilty is  .
.
| Name |
|---|




