| Codeforces Round 419 (Div. 1) |
|---|
| Finished |
On the way to school, Karen became fixated on the puzzle game on her phone!

The game is played as follows. In each level, you have a grid with n rows and m columns. Each cell originally contains the number 0.
One move consists of choosing one row or column, and adding 1 to all of the cells in that row or column.
To win the level, after all the moves, the number in the cell at the i-th row and j-th column should be equal to gi, j.
Karen is stuck on one level, and wants to know a way to beat this level using the minimum number of moves. Please, help her with this task!
The first line of input contains two integers, n and m (1 ≤ n, m ≤ 100), the number of rows and the number of columns in the grid, respectively.
The next n lines each contain m integers. In particular, the j-th integer in the i-th of these rows contains gi, j (0 ≤ gi, j ≤ 500).
If there is an error and it is actually not possible to beat the level, output a single integer -1.
Otherwise, on the first line, output a single integer k, the minimum number of moves necessary to beat the level.
The next k lines should each contain one of the following, describing the moves in the order they must be done:
- row x, (1 ≤ x ≤ n) describing a move of the form "choose the x-th row".
- col x, (1 ≤ x ≤ m) describing a move of the form "choose the x-th column".
If there are multiple optimal solutions, output any one of them.
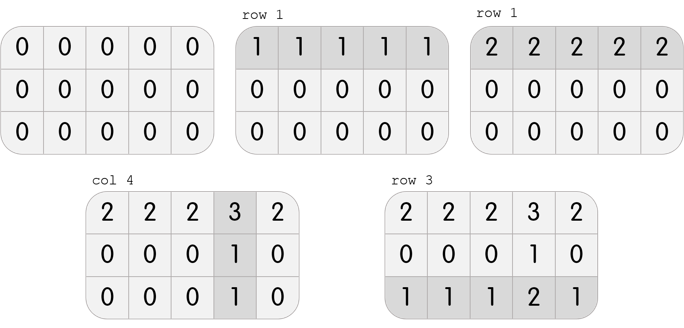
3 5
2 2 2 3 2
0 0 0 1 0
1 1 1 2 1
4
row 1
row 1
col 4
row 3
3 3
0 0 0
0 1 0
0 0 0
-1
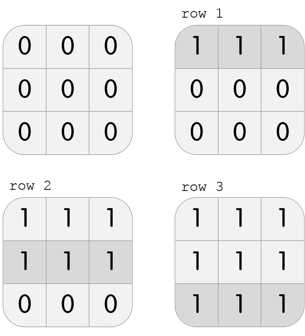
3 3
1 1 1
1 1 1
1 1 1
3
row 1
row 2
row 3
In the first test case, Karen has a grid with 3 rows and 5 columns. She can perform the following 4 moves to beat the level:
In the second test case, Karen has a grid with 3 rows and 3 columns. It is clear that it is impossible to beat the level; performing any move will create three 1s on the grid, but it is required to only have one 1 in the center.
In the third test case, Karen has a grid with 3 rows and 3 columns. She can perform the following 3 moves to beat the level:
Note that this is not the only solution; another solution, among others, is col 1, col 2, col 3.
| Name |
|---|




