| Good Bye 2017 |
|---|
| Finished |
You are given three integers k, pa and pb.
You will construct a sequence with the following algorithm: Initially, start with the empty sequence. Each second, you do the following. With probability pa / (pa + pb), add 'a' to the end of the sequence. Otherwise (with probability pb / (pa + pb)), add 'b' to the end of the sequence.
You stop once there are at least k subsequences that form 'ab'. Determine the expected number of times 'ab' is a subsequence in the resulting sequence. It can be shown that this can be represented by P / Q, where P and Q are coprime integers, and  . Print the value of
. Print the value of 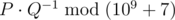 .
.
The first line will contain three integers integer k, pa, pb (1 ≤ k ≤ 1 000, 1 ≤ pa, pb ≤ 1 000 000).
Print a single integer, the answer to the problem.
1 1 1
2
3 1 4
370000006
The first sample, we will keep appending to our sequence until we get the subsequence 'ab' at least once. For instance, we get the sequence 'ab' with probability 1/4, 'bbab' with probability 1/16, and 'aab' with probability 1/8. Note, it's impossible for us to end with a sequence like 'aabab', since we would have stopped our algorithm once we had the prefix 'aab'.
The expected amount of times that 'ab' will occur across all valid sequences is 2.
For the second sample, the answer is equal to 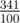 .
.
| Name |
|---|




