| Hello 2018 |
|---|
| Finished |
You generate real numbers s1, s2, ..., sn as follows:
- s0 = 0;
- si = si - 1 + ti, where ti is a real number chosen independently uniformly at random between 0 and 1, inclusive.
You are given real numbers x1, x2, ..., xn. You are interested in the probability that si ≤ xi is true for all i simultaneously.
It can be shown that this can be represented as 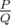 , where P and Q are coprime integers, and
, where P and Q are coprime integers, and 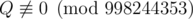 . Print the value of P·Q - 1 modulo 998244353.
. Print the value of P·Q - 1 modulo 998244353.
The first line contains integer n (1 ≤ n ≤ 30).
The next n lines contain real numbers x1, x2, ..., xn, given with at most six digits after the decimal point (0 < xi ≤ n).
Print a single integer, the answer to the problem.
4
1.00
2
3.000000
4.0
1
1
0.50216
342677322
2
0.5
1.0
623902721
6
0.77
1.234567
2.1
1.890
2.9999
3.77
859831967
In the first example, the sought probability is 1 since the sum of i real numbers which don't exceed 1 doesn't exceed i.
In the second example, the probability is x1 itself.
In the third example, the sought probability is 3 / 8.
| Name |
|---|




