There is a matrix A of size x × y filled with integers. For every 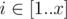 ,
, 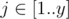 Ai, j = y(i - 1) + j. Obviously, every integer from [1..xy] occurs exactly once in this matrix.
Ai, j = y(i - 1) + j. Obviously, every integer from [1..xy] occurs exactly once in this matrix.
You have traversed some path in this matrix. Your path can be described as a sequence of visited cells a1, a2, ..., an denoting that you started in the cell containing the number a1, then moved to the cell with the number a2, and so on.
From the cell located in i-th line and j-th column (we denote this cell as (i, j)) you can move into one of the following cells:
- (i + 1, j) — only if i < x;
- (i, j + 1) — only if j < y;
- (i - 1, j) — only if i > 1;
- (i, j - 1) — only if j > 1.
Notice that making a move requires you to go to an adjacent cell. It is not allowed to stay in the same cell. You don't know x and y exactly, but you have to find any possible values for these numbers such that you could start in the cell containing the integer a1, then move to the cell containing a2 (in one step), then move to the cell containing a3 (also in one step) and so on. Can you choose x and y so that they don't contradict with your sequence of moves?
The first line contains one integer number n (1 ≤ n ≤ 200000) — the number of cells you visited on your path (if some cell is visited twice, then it's listed twice).
The second line contains n integers a1, a2, ..., an (1 ≤ ai ≤ 109) — the integers in the cells on your path.
If all possible values of x and y such that 1 ≤ x, y ≤ 109 contradict with the information about your path, print NO.
Otherwise, print YES in the first line, and in the second line print the values x and y such that your path was possible with such number of lines and columns in the matrix. Remember that they must be positive integers not exceeding 109.
8
1 2 3 6 9 8 5 2
YES
3 3
6
1 2 1 2 5 3
NO
2
1 10
YES
4 9
The matrix and the path on it in the first test looks like this:
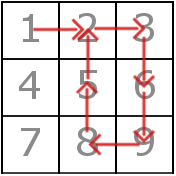
Also there exist multiple correct answers for both the first and the third examples.
| Name |
|---|




