| Yandex.Algorithm 2011: Finals |
|---|
| Finished |
One university has just found out about a sport programming contest called ACM ICPC v2.0. This contest doesn't differ much from the well-known ACM ICPC, for example, the participants are not allowed to take part in the finals more than two times. However, there is one notable difference: the teams in the contest should consist of exactly n participants.
Having taken part in several ACM ICPC v2.0 finals and having not won any medals, the students and the university governors realized that it's high time they changed something about the preparation process. Specifically, as the first innovation it was decided to change the teams' formation process. Having spent considerable amount of time on studying the statistics of other universities' performance, they managed to receive some interesting information: the dependence between the probability of winning a medal and the number of team members that participated in the finals in the past. More formally, we know n + 1 real numbers p0 ≤ p1 ≤ ... ≤ pn, where pi is the probability of getting a medal on the finals if the team has i participants of previous finals, and other n - i participants arrived to the finals for the first time.
Despite such useful data, the university governors are unable to determine such team forming tactics that would provide the maximum probability of winning a medal at ACM ICPC v2.0 finals on average (we are supposed to want to provide such result to the far future and we are also supposed to have an endless supply of students). And how about you, can you offer such optimal tactic? At the first stage the university governors want to know the value of maximum average probability.
More formally, suppose that the university sends a team to the k-th world finals. The team has ak participants of previous finals (0 ≤ ak ≤ n). Since each person can participate in the finals no more than twice, the following condition must be true:  . Your task is to choose sequence
. Your task is to choose sequence  so that the limit Ψ exists and it's value is maximal:
so that the limit Ψ exists and it's value is maximal:
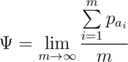
As  is an infinite sequence, you should only print the maximum value of the Ψ limit.
is an infinite sequence, you should only print the maximum value of the Ψ limit.
The first line contains an integer n (3 ≤ n ≤ 100), n is the number of team participants. The second line contains n + 1 real numbers with no more than 6 digits after decimal point pi (0 ≤ i ≤ n, 0 ≤ pi ≤ 1) — the probability of that the team will win a medal if it contains i participants who has already been on the finals. Also the condition pi ≤ pi + 1 should be fulfilled for all 0 ≤ i ≤ n - 1.
Print the only real number — the expected average number of medals won per year if the optimal strategy is used. The result may have absolute or relative error 10 - 6.
3
0.115590 0.384031 0.443128 0.562356
0.4286122500
3
1 1 1 1
0.9999999999
In the second test, no matter what participants the team contains, it is doomed to be successful.
| Name |
|---|




