| Codeforces Round 490 (Div. 3) |
|---|
| Finished |
There are $$$n$$$ cities and $$$m$$$ roads in Berland. Each road connects a pair of cities. The roads in Berland are one-way.
What is the minimum number of new roads that need to be built to make all the cities reachable from the capital?
New roads will also be one-way.
The first line of input consists of three integers $$$n$$$, $$$m$$$ and $$$s$$$ ($$$1 \le n \le 5000, 0 \le m \le 5000, 1 \le s \le n$$$) — the number of cities, the number of roads and the index of the capital. Cities are indexed from $$$1$$$ to $$$n$$$.
The following $$$m$$$ lines contain roads: road $$$i$$$ is given as a pair of cities $$$u_i$$$, $$$v_i$$$ ($$$1 \le u_i, v_i \le n$$$, $$$u_i \ne v_i$$$). For each pair of cities $$$(u, v)$$$, there can be at most one road from $$$u$$$ to $$$v$$$. Roads in opposite directions between a pair of cities are allowed (i.e. from $$$u$$$ to $$$v$$$ and from $$$v$$$ to $$$u$$$).
Print one integer — the minimum number of extra roads needed to make all the cities reachable from city $$$s$$$. If all the cities are already reachable from $$$s$$$, print 0.
9 9 1
1 2
1 3
2 3
1 5
5 6
6 1
1 8
9 8
7 1
3
5 4 5
1 2
2 3
3 4
4 1
1
The first example is illustrated by the following:
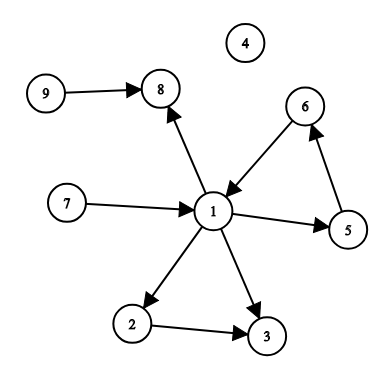
For example, you can add roads ($$$6, 4$$$), ($$$7, 9$$$), ($$$1, 7$$$) to make all the cities reachable from $$$s = 1$$$.
The second example is illustrated by the following:
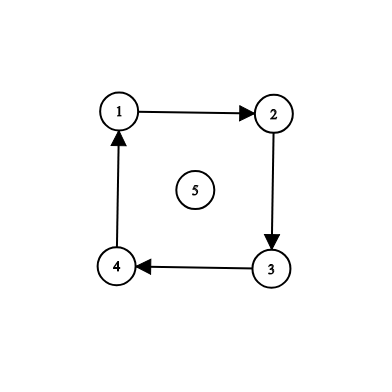
In this example, you can add any one of the roads ($$$5, 1$$$), ($$$5, 2$$$), ($$$5, 3$$$), ($$$5, 4$$$) to make all the cities reachable from $$$s = 5$$$.
| Name |
|---|




