550A - Two Substrings
There are many ways to solve this problem. Author solution does the following: check if substring "AB" goes before "BA", and then vice versa, if "BA" goes before "AB".
You can do it in the following way: find the first occurence of "AB" then check all substrings of length two to the right of it to check if substring "BA" also exists. Then do it vice versa.
Complexity of the solution is O(n), where n is the length of the given string.
550B - Preparing Olympiad
Because of the low constraints, this problem can be solved by complete search over all problem sets (there are 2n of them).
For every potential problem set (which can be conviniently expressed as bit mask) we need to check if it satisfies all needed criteria. We can simply find the sum of problem complexities and also the difference between the most difficult and the easiest problems in linear time, iterating over the problems that we included in our current set/bitmask. If this problem set can be used, we increase the answer by one.
Complexity of this solution is O(2n·n).
550C - Divisibility by Eight
This problem can be solved with at least two different approaches.
The first one is based on the "school" property of the divisibility by eight — number can be divided by eight if and only if its last three digits form a number that can be divided by eight. Thus, it is enough to test only numbers that can be obtained from the original one by crossing out and that contain at most three digits (so we check only all one-digit, two-digit and three-digit numbers). This can be done in O(len3) with three nested loops (here len is the length of the original number).
Second approach uses dynamic programming. Let's calculate dp[i][j], 1 ≤ i ≤ n, 0 ≤ j < 8. The value of dp is true if we can cross out some ditits from the prefix of length i such that the remaining number gives j modulo eight, and false otherwise.
This dp can be calculated in the following way: let ai be ith digit of the given number. Then dp[i][aimod8] = 1 (just this number). For all 0 ≤ j < 8 dp[i][(j * 10 + ai)mod8] = max(dp[i][(j * 10 + ai)mod8], dp[i - 1][j]) (we add current digit to some previous result), dp[i][(j * 10)mod8] = max(dp[i][(j * 10)mod8], dp[i - 1][j]) (we cross out current digit).
Answer is "YES" if dp[i][0] = 1 for some position i. For restoring the answer we need to keep additional array prev[i][j], which will say from where current value was calculated. Complexity of such solution is O(8·len) (again len is the length of the original number).
550D - Regular Bridge
Let's prove that there is no solution for even k.
Suppose our graph contains some bridges, k = 2s (even), all degrees are k. Then there always exists strongly connected component that is connected to other part of the graph with exactly one bridge.
Consider this component. Let's remove bridge that connects it to the remaining graph. Then it has one vertex with degree k - 1 = 2s - 1 and some vertices with degrees k = 2s. But then the graph consisting of this component will contain only one vertex with odd degree, which is impossible by Handshaking Lemma.
Let's construct the answer for odd k. Let k = 2s - 1.
For k = 1 graph consisting of two nodes connected by edge works.
For k ≥ 3 let's construct graph with 2k + 4 nodes. Let it consist of two strongly connected components connected by bridge. Enumerate nodes of first component from 1 to k + 2, second component will be the same as the first one.
Let vertex 1 be connected to the second component by bridge. Also connect it with k - 1 edges to vertices 2, 3, ..., k. Connect vertices 2, 3, ..., k to each other (add all possible edges between them), and then remove edges between every neighbouring pair, for example edges 2 - 3, 4 - 5, ..., (k - 1) - k.
Then we connect vertices 2, 3, ..., k with vertices k + 1 and k + 2. And finally add an edge between nodes k + 1 and k + 2.
Build the second component in the similar manner, and add a bridge between components. Constructed graph has one bridge, all degrees of k and consists of O(k) nodes and O(k2) edges.
Complexity of the solution — O(k2).
550E - Brackets in Implications
Let input consists of 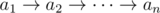 , ai is 0 or 1 for all i.
, ai is 0 or 1 for all i.
Let's show that there is no solution in only two cases:
1) an = 1.
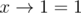 , for all x, and no parentheses can change last 1 to 0.
, for all x, and no parentheses can change last 1 to 0.
2) Input has the form  or its suffix with at least two arguments.
or its suffix with at least two arguments.
This can be proven by induction. For input  there is no solution, for longer inputs any attempt to put parentheses will decrease the number of 1s in the beginning by one, or will introduce 1 in the last position (which will lead to case one).
there is no solution, for longer inputs any attempt to put parentheses will decrease the number of 1s in the beginning by one, or will introduce 1 in the last position (which will lead to case one).
Let's construct solution for all other cases.
1) For input 0 we don't need to do anything.
2) For input of the form 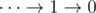 we don't need any parentheses, the value of this expression is always
we don't need any parentheses, the value of this expression is always
3) Expression in the form  (where second missed part consists of ones only). Then
(where second missed part consists of ones only). Then  .
.
Complexity of the solution is O(n).






