One can notice that the maximum cost of sending a letter from i'th city is equal to maximum of distances from i'th city to first city and from i'th city to last (max(abs(xi - x0), abs(xi - xn - 1)). On the other hand, the minimum cost of sending a letter will be the minimum of distances between neighboring cities (i - 1'th and i + 1'th cities), more formally, min(abs(xi - xi - 1), abs(xi - xi + 1). For each city, except the first and the last this formula is correct, but for them formulas are (abs(xi - xi + 1)) and (abs(xi - xi - 1)) respectively.
567B - Berland National Library
To answer the queries correct, we need to know if the person is still in the library. For that purpose we will use in array of type bool. Also we will store two variables for the answer and ''current state'' (it will store the current number of people in the library). Let's call them ans and state respectively.
Thus, if we are given query + ai then we should increase state by one, mark that this person entered the library (in[ai] = true) and try to update the answer (ans = max(ans, state)).
Otherwise we are given - ai query. If the person who leaves the library, was in there, we should just decrease state by one. Otherwise, if this person was not in the library (in[ai] == false) and leaves now, he entered the library before we started counting. It means we should increase the answer by one anyway. Also one should not forget that it is needed to mark that the person has left the library (in[ai] = false).
Let's solve this problem for fixed middle element of progression. This means that if we fix element ai then the progression must consist of ai / k and ai·k elements. It could not be possible, for example, if ai is not divisible by k (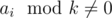 ).
).
For fixed middle element one could find the number of sequences by counting how many ai / k elements are placed left from fixed element and how many ai·k are placed right from it, and then multiplying this numbers. To do this, one could use two associative arrays Al and Ar, where for each key x will be stored count of occurences of x placed left (or right respectively) from current element. This could be done with map structure.
Sum of values calculated as described above will give the answer to the problem.
567D - One-Dimensional Battle Ships
First, we should understand when the game ends. It will happen when on the n-sized board it will be impossible to place k ships of size a. For segment with length len we could count the maximum number of ships with size a that could be placed on it. Each ship occupies a + 1 cells, except the last ship. Thus, for segment with length len the formula will look like 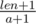 (we add "fictive" cell to len cells to consider the last ship cell). This way, for [l..r] segment the formula should be
(we add "fictive" cell to len cells to consider the last ship cell). This way, for [l..r] segment the formula should be 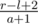 .
.
For solving the problem we should store all the [l..r] segments which has no ''free'' cells (none of them was shooted). One could use (std: : set) for that purpose. This way, before the shooting, there will be only one segment [1..n]. Also we will store current maximum number of ships we could place on a board. Before the shooting it is equal to 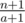 .
.
With every shoot in cell x we should find the segment containing shooted cell (let it be [l..r]), we should update segment set. First, we should delete [l..r] segment. It means we should decrease current maximum number of ships by 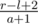 and delete it from the set. Next, we need to add segments [l..x - 1] and [x + 1..r] to the set (they may not be correct, so you may need to add only one segments or do not add segments at all) and update the maximum number of ships properly. We should process shoots one by one, and when the maximum number of ships will become lesser than k, we must output the answer. If that never happen, output - 1.
and delete it from the set. Next, we need to add segments [l..x - 1] and [x + 1..r] to the set (they may not be correct, so you may need to add only one segments or do not add segments at all) and update the maximum number of ships properly. We should process shoots one by one, and when the maximum number of ships will become lesser than k, we must output the answer. If that never happen, output - 1.
At first, let's find edges that do not belong to any shortest paths from s to t. Let's find two shortest path arrays d1 and d2 with any shortest-path-finding algorithm. First array stores shortest path length from s, and the second — from t. Edge (u, v) then will be on at least one shortest path from s to t if and only if d1[u] + w(u, v) + d2[v] == d1[t].
Let's build shortest path graph, leaving only edges described above. If we consider shortest path from s to t as segment [0..D] and any edge (u, v) in shortest path graph as its subsegment [d1[u]..d1[v]], then if such subsegment do not share any common point with any other edge subsegment, except its leftest and rightest point (d1[u] and d1[v]), this edge belongs to every shortest path from s to t.
Now we could surely answer "YES" to such edges. Next part of the solution are much simple. If edge (u, v) do not belong to every shortest path, we could try decrease its weight. This edge will belong to every shortest path if and only if its weight will become d1[t] - d1[u] - d2[v] - 1. So, if this value are strictly positive, we should answer "CAN" considering new edge weight. Otherwise we need to output "NO".
Consider that we are placing blocks by pairs, one pair by one, starting from leftmost and rightmost places. Thus, for example, two blocks of height 1 we could place in positions 1 and 2, 1 and 2n, or 2n - 1 and 2n. The segment of unused positions will be changed that way and the next block pairs should be placed on new leftmost and rightmost free places. At last only two positions will be free and we should place two blocks of height n on them.
Any correct sequence of blocks could be builded that way. Let's try to review the requirements consider such way of placing blocks. As soon as we place blocks one by one, the requirements are now only describes the order of placing blocks. For example, requirement ''3 >= 5'' means that we should place block in position 3 only if block in position 5 is already placed (and thus it have lesser height), or we place pair of blocks of same height on them at one moment.
For counting required number of sequences we will use dynamic programming approach. Let's count dp[l][r] — the number of ways to place some blocks in the way that only positions at segment [l..r] are free. The height of current placed pair of blocks is counted from the segment borders itself (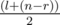 . Fix one way of placing current block pair (exclusion is l = = r + 1). Now check if such placing meets the requirements. We will consider only requirements that meets one of the current-placing positions. For every "current" position "<" must be true only for free positions (positions in [l..r], which do not equal to current positions), ">" must be true for already-placed positions (out of [l..r]) and "=" must be true only for second current position.
. Fix one way of placing current block pair (exclusion is l = = r + 1). Now check if such placing meets the requirements. We will consider only requirements that meets one of the current-placing positions. For every "current" position "<" must be true only for free positions (positions in [l..r], which do not equal to current positions), ">" must be true for already-placed positions (out of [l..r]) and "=" must be true only for second current position.
This DP could be easily calculated using "lazy" approach.







