593A - 2Char
For each letter will maintain the total length of words (cnt1ci), which found it was alone, and for each pair of letters will maintain the total length of words that contains only them (cnt2ci, cj).
For each row, count a number of different letters in it. If it is one, then add this letter to the length of the word. If two of them, then add to the pair of letters word`s length.
Now find a pair of letters that will be the answer. For a pair of letters ci, cj answer is cnt1ci + cnt1cj + cnt2ci, cj. Among all these pairs find the maximum. This is the answer.
The overall complexity is O (total length of all strings + 26 * 26)
593B - Anton and Lines
Note that if a s line intersects with the j th in this band, and at x = x1 i th line is higher, at x = x2 above would be j th line. Sort by y coordinate at x = x1 + eps, and x = x2 - eps. Verify that the order of lines in both cases is the same. If there is a line that its index in the former case does not coincide with the second, output Yes. In another case, derive No. The only thing that can stop us is the intersection at the borders, as in this case we dont know the sorts order. Then add to our border x1 small eps, and by x2 subtract eps, and the sort order is set uniquely. The overall complexity is O(nlogn)
593C - Beautiful Function
One of the answers will be the amount of such expressions for each circle in the coordinate x and similarly coordinate y: 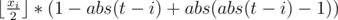
For a = 1, b = abs(t - i), it can be written as 
Consider the a - b + abs(a - b):
if a ≤ b, то a - b + abs(a - b) = 0,
if a > b, то a - b + abs(a - b) = 2a - 2b
Now consider what means a > b:
1 > abs(t - i)
i > t - 1 and i < t + 1.
For integer i is possible only if i = t.
That is, this bracket is not nullified only if i = t.
Consider the 2a - 2b = 2 - 2 * abs(t - i) = 2. Then 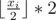 differs from the wanted position by no more than 1, but since all the radiuses are not less than 2, then this point belongs to the circle.
differs from the wanted position by no more than 1, but since all the radiuses are not less than 2, then this point belongs to the circle.
The overall complexity is O(n).
593D - Happy Tree Party
Consider the problem ignoring the second typed requests. We note that in the column where all the numbers on the edges of > 1 maximum number of assignments to 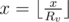 before x will turn into 0 is not exceeds 64. Indeed, if all the Rv = 2, the number of operations can be assessed as log2(x). Hang the tree for some top and call it the root.
before x will turn into 0 is not exceeds 64. Indeed, if all the Rv = 2, the number of operations can be assessed as log2(x). Hang the tree for some top and call it the root.
Learn how to solve the problem, provided that for every v Rv > 1 and no requests of the second type. For each vertex except the root, we have identified it as the ancestor of the neighbor closest to the root. Suppose we had a request of the first type from the top a to b vertices with original number x. We divide the road into two vertical parts, one of which is close to the root, while the other moves away. We find all the edges in this way. To do this, we calculate the depth of each node to the root of the distance. Now we will go up in parallel to the tree of the two peaks, until he met a total. If in the course of the recovery, we have been more than 64 edges, in the substitutions 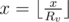 we get x = 0 and we can at the current step to stop the algorithm search. Thus, we make no more than O(log(x)) operations.
we get x = 0 and we can at the current step to stop the algorithm search. Thus, we make no more than O(log(x)) operations.
Let`s turn to the problem, where Rv > 0. We note that our previous solution in this case can work for O(n). Since the passage of the edge with Rv = 1 our value does not change. We reduce this problem to the above consideration. Compress the graph, that is, remove all single edges. To do this, run by dfs root and will keep the deepest edge on the path from the root to the top with Rv > 1.
Let us remember that we have had requests to reduce Rv. We maintain the closest ancestor of Pv c RPv > 1. We use the idea of compression paths. When answer to a request of the first type will be recalculated Pv. We introduce a recursive function F(v). Which returns the v, if Rv > 1, otherwise perform the assignment of Pv = F(Pv) and returns F(Pv). Each edge we will remove 1 times, so in total the call of all functions F(v) running O(n).
Final time is O(logx) on request of the first type and O(1) an average of request of the second type.
593E - Strange Calculation and Cats
Learn how to solve the problem for small t. We use standard dynamic dpx, y, t = number of ways to get into the cell (x; y) at time t. Conversion is the sum of all valid ways to get into the cell (x; y) at time t — 1.
Note that this dp can be counted by means of the construction of the power matrix. Head of the transition matrix, Ti, j = 1, if we can get out of the cell i in a cell j. Suppose we had a vector G, where Gi equal to the number of ways to get into the cell i. Then a new vector G' by dt second G' = G * (Tdt).
So we learned to solve the problem without changes in O (log dt * S3), where dt — at a time, S — area.
Consider what happens when adding or removing a cat. When such requests varies transition matrix. Between these requests constant T, then we can construct a power matrix. Thus, at the moment of change is recalculated T, and between changes in the degree of erecting matrix. The decision is O (m * S3 log dt), m — number of requests







