621A - Мокрая Акула и чётность
First, if the sum of all the numbers is already even, then we do nothing. Otherwise, we remove the smallest odd number. Since, if the sum is odd, we need to remove a number with the same parity to make the sum even. Notice it's always bad to remove more odd numbers, and it does nothing to remove even numbers.
Let's start with two bishops (x1, y1) and (x2, y2). Notice that if (x1, y1) attacks (x2, y2), either x1 + y1 == x2 + y2 OR x1 — y1 == x2 — y2. So, for each bishop (x, y), we will store x + y in one map and x — y in another map.
Let f(x) be the probability that the product of the number of flowers of sharks x and 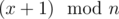 is divisible by p.
is divisible by p.
We want the expected value of the number of pairs of neighbouring sharks whose flower numbers are divisible by p. From linearity of expectation, this is equal to the probabilities that each pair multiplies to a number divisible by p, or f(0) + f(1) + ... + f(n). (Don't forget about the wrap-around at n)
Now, for each pair of neighbouring sharks, we need to figure out the probability that their product is divisible by p. Consider an interval [li, ri]. How many numbers in this interval are divisible by p? Well, it is easier if we break the interval [li, ri] up into [1, ri] - [1, li - 1]. Since 1, 2, ..., x contains 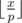 numbers divisible by p, the interval [li, ri] contains
numbers divisible by p, the interval [li, ri] contains 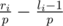 numbers divisible by p.
numbers divisible by p.
Now, consider two numbers 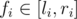 and
and 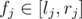 , with
, with 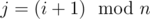 . Let ai be the number of integers divisible by p in the interval [li, ri], and define aj similarly. Now what's the probability that fi·fj is divisible by p? We can count the opposite: the probability that fi·fj is not divisible by p. Since p is a prime, this means neither fi nor fj is divisible by p. The number of integers in [li, ri] not divisible by p is ri - li + 1 - ai. Similar for j. Therefore, the probability fi·fj is not divisible by p is given by
. Let ai be the number of integers divisible by p in the interval [li, ri], and define aj similarly. Now what's the probability that fi·fj is divisible by p? We can count the opposite: the probability that fi·fj is not divisible by p. Since p is a prime, this means neither fi nor fj is divisible by p. The number of integers in [li, ri] not divisible by p is ri - li + 1 - ai. Similar for j. Therefore, the probability fi·fj is not divisible by p is given by 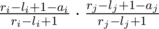 . Therefore, the probability it is can be given by
. Therefore, the probability it is can be given by 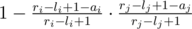 . Now, just sum over this for all i.
. Now, just sum over this for all i.
The tricky Rat Kwesh has finally made an appearance; it is time to prepare for some tricks. But truly, we didn't expect it to be so hard for competitors though. Especially the part about taking log of a negative number.
We need a way to deal with xyz and xyz. We cannot directly compare them, 200200200 is way too big. So what we do? Take log! 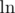 is an increasing function on positive numbers (we can see this by taking
is an increasing function on positive numbers (we can see this by taking 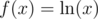 , then
, then 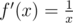 , which is positive when we are dealing with positive numbers). So if
, which is positive when we are dealing with positive numbers). So if 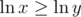 , then x ≥ y.
, then x ≥ y.
When we take log, 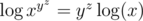 But yz can still be 200200, which is still far too big. So now what can we do? Another log! But is it legal? When x = 0.1 for example,
But yz can still be 200200, which is still far too big. So now what can we do? Another log! But is it legal? When x = 0.1 for example, 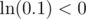 , so we cannot take another log. When can we take another log, however? We need
, so we cannot take another log. When can we take another log, however? We need 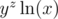 to be a positive number. yz will always be positive, so all we need is for
to be a positive number. yz will always be positive, so all we need is for 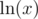 to be positive. This happens when x > 1. So if x, y, z > 1, everything will be ok.
to be positive. This happens when x > 1. So if x, y, z > 1, everything will be ok.
There is another good observation to make. If one of x, y, z is greater than 1, then we can always achieve some expression (out of those 12) whose value is greater than 1. But if x < 1, then xa will never be greater than 1. So if at least one of x, y, z is greater than 1, then we can discard those bases that are less than or equal to 1. In this case, 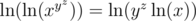 . Remember that
. Remember that 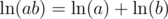 , so
, so 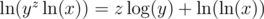 . Similarly,
. Similarly, 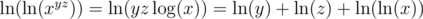 .
.
The last case is when x ≤ 1, y ≤ 1, z ≤ 1. Then, notice that for example, 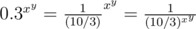 . But the denominator of this fraction is something we recognize, because 10 / 3 > 1. So if all x, y, z < 1, then it is the same as the original problem, except we are looking for the minimum this time.
. But the denominator of this fraction is something we recognize, because 10 / 3 > 1. So if all x, y, z < 1, then it is the same as the original problem, except we are looking for the minimum this time.
First, let us build an X by X matrix. We will be applying matrix exponentiation on this matrix. For each modulo value T from 0 to X — 1, and each value in the array with index i between 1 and n, we will do: matrix[T][(10 * T + arr[i]) % X]++. This is because, notice that for each block we allow one more way to go between a modulo value T, and (10 * T + arr[i]) % X. We are multiplying T by 10 because we are "left-shifting" the number in a way (i.e. changing 123 -> 1230), and then adding arr[i] to it. Notice that this basically simulates the concatenation that Wet Shark is conducting, without need of a brute force dp approach.





