Hello Codeforces,
Recently I decided to start learning geometry so I found out that I have to start with the simple geometry, basic shapes, basic laws and cakewalk problems to set off my journey with geometry and computational geometry then, so I came across this problem from the gym,
Given a circle (the center of the circle |x|,|y| <= 1000, and the radius r <= 10000) .
Given a rectangle (the coordinates of the bottom-left corner and the upper-right corner, |x|,|y| <= 1000 as well) .
It's guaranteed that the upper-left corner of the rectangle is inside the circle, the width and the height of the rectangle are longer than 2.r .
you're to calculate the area of the intersection between the circle and the rectangle .
Here's what I did :
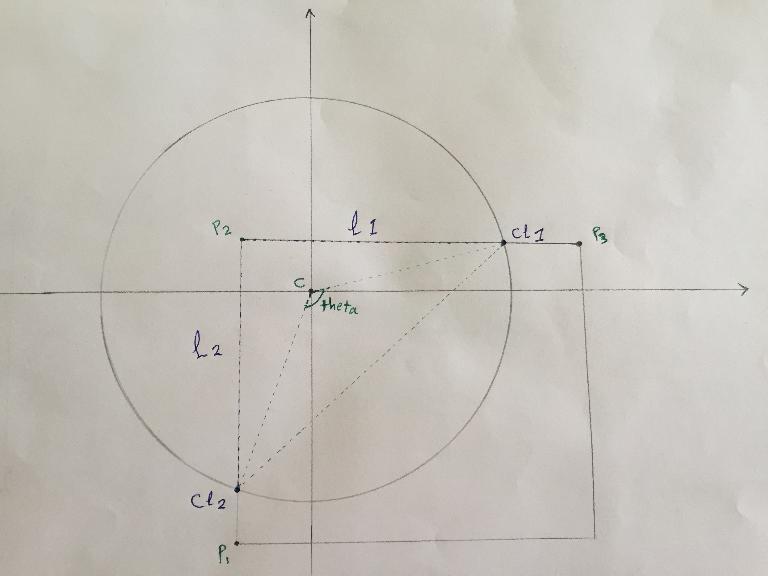
- Obtain the two lines P2-P3 let's say L1 and P2-P1 let's say L2 .
- Find the points of the intersection between the lines L1,L2 and the the circle, They're CL1, CL2 .
- Compute the angle (CL1 C CL2) theta .
- Compute the area of the circular sector determined by theta, say A .
- Subtract the area of the triangle (CL1 C CL2) from A .
- Add the area of the triangle (CL1 P2 CL2) to A and A is the answer .
So I keep getting WA for the couple past days. Since it's being the first time I write a geometry code I know it'd be so buggy and really it was, I've been debugging it for hours and I re-wrote it several times, and eventually I had no thing to do with it, I badly ran out of my shots :(
Here's my code .
It would be really appreciated if someone tells me what's going wrong (maybe it's my algorithm though, Now I doubt it's absolutely correct) Thanks in advance .
By the way, any advice, references, and problems would help a noob to kick-off in geometry would be highly appreciated as well .
→ Pay attention
→ Streams
→ Top rated
| # | User | Rating |
|---|---|---|
| 1 | ecnerwala | 3649 |
| 2 | Benq | 3581 |
| 3 | orzdevinwang | 3570 |
| 4 | Geothermal | 3569 |
| 4 | cnnfls_csy | 3569 |
| 6 | tourist | 3565 |
| 7 | maroonrk | 3531 |
| 8 | Radewoosh | 3521 |
| 9 | Um_nik | 3482 |
| 10 | jiangly | 3468 |
→ Top contributors
| # | User | Contrib. |
|---|---|---|
| 1 | maomao90 | 174 |
| 2 | awoo | 164 |
| 3 | adamant | 162 |
| 4 | TheScrasse | 159 |
| 5 | nor | 158 |
| 6 | maroonrk | 156 |
| 7 | -is-this-fft- | 151 |
| 8 | SecondThread | 147 |
| 9 | orz | 146 |
| 10 | pajenegod | 145 |
→ Find user
→ Recent actions
Help In A Simple Geometry Problem
Revision en2, by yashi, 2016-04-08 01:03:36
History
Codeforces (c) Copyright 2010-2024 Mike Mirzayanov
The only programming contests Web 2.0 platform
Server time: Apr/25/2024 19:00:42 (k3).
Desktop version, switch to mobile version.
Supported by
User lists


| Name |
|---|






