665F - Four Divisors
The editorial for this problem is a little modification of the materials from the lecture of Mikhail Tikhomirov Endagorion of the autumn of 2015 in Moscow Institute of Physics and Technology. Thanks a lot to Endagorion for that materials.
Easy to see that only the number of the form p·q and p3 (for different prime p, q) have exactly four positive divisors.
We can easily count the numbers of the form p3 in 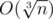 , where n is the number from the problem statement.
, where n is the number from the problem statement.
Now let p < q and π(k) be the number of primes from 1 to k. Let's iterate over all the values p. Easy to see that 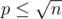 . So for fixed p we should increase the answer by the value
. So for fixed p we should increase the answer by the value 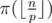 .
.
So the task is ot to find 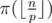 ~--- the number of primes not exceeding
~--- the number of primes not exceeding  , for all p.
, for all p.
Denote pj the j-th prime number. Denote dpn, j the number of k such that 1 ≤ k ≤ n, and all prime divisors of k are at least pj (note that 1 is counted in all dpn, j, since the set of its prime divisors is empty). dpn, j satisfy a simple recurrence:
dpn, 1 = n (since p1 = 2)
dpn, j = dpn, j + 1 + dp⌊ n / pj⌋, j, hence dpn, j + 1 = dpn, j - dp⌊ n / pj⌋, j
Let pk be the smallest prime greater than  . Then π(n) = dpn, k + k - 1 (by definition, the first summand accounts for all the primes not less than k).
. Then π(n) = dpn, k + k - 1 (by definition, the first summand accounts for all the primes not less than k).
If we evaluate the recurrence dpn, k straightforwardly, all the reachable states will be of the form dp⌊ n / i⌋, j. We can also note that if pj and pk are both greater than  , then dpn, j + j = dpn, k + k. Thus, for each ⌊ n / i⌋ it makes sense to keep only
, then dpn, j + j = dpn, k + k. Thus, for each ⌊ n / i⌋ it makes sense to keep only  values of dp⌊ n / i⌋, j.
values of dp⌊ n / i⌋, j.
Instead of evaluating all DP states straightforwardly, we perform a two-step process:
Choose K.
Run recursive evaluation of dpn, k. If we want to compute a state with n < K, memorize the query ``count the numbers not exceeding n with all prime divisors at least k''.
Answer all the queries off-line: compute the sieve for numbers up to K, then sort all numbers by the smallest prime divisor. Now all queries can be answered using RSQ structure. Store all the answers globally.
Run recurisive evaluation of dpn, k yet again. If we want to compute a state with n < K, then we must have preprocessed a query for this state, so take it from the global set of answers.
The performance of this approach relies heavily on Q~--- the number of queries we have to preprocess.
Statement. 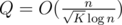 .
.
Proof:
Each state we have to preprocess is obtained by following a dp⌊ n / pj⌋, j transition from some greater state. It follows that Q doesn't exceed the total number of states for n > K.
[Q \leq \sum_{j = 1}^{n / K} \pi(\sqrt{n / j}) \sim \sum_{j = 1}^{n / K} \sqrt{n / j} / \log n \sim \frac{1}{\log n}\int_1^{n / K} \sqrt{n / x} dx \sim \frac{n}{\sqrt{K}\log n}]
The preprocessing of Q queries can be done in 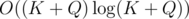 , and it is the heaviest part of the computation. Choosing optimal
, and it is the heaviest part of the computation. Choosing optimal 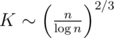 , we obtain the complexity
, we obtain the complexity 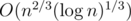 .
.
Complexity: 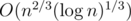 .
.







