I got to IOI solving — and upsolving — a bit late and I just recently finished it (with help of various comments). One thing I didn't really see there was: how would you have done?
Here are my comments about the problems:
aliens: a common DP + convex hull trick; apparently,
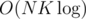 gets TLE for the 5th subtask and even O(NK) has trouble fitting within the TL; 60pts
gets TLE for the 5th subtask and even O(NK) has trouble fitting within the TL; 60ptsshortcut: I knew that there's binsearch (from a similar TC problem); afterwards, finding an
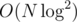 solution isn't hard, but improving it enough to get more points is; 93pts
solution isn't hard, but improving it enough to get more points is; 93ptsrailroad: mfw — I didn't move beyond a bitset DP; even though I had a lot of ideas including what turned out to be the correct one (finding a flow), I thought it'd be some kind of greedy, but those are numerous and hard to check in this case; the last subtask was very easy after solving the 3rd; 34pts
messy: the bounds are 7·27 with N = 27, so it has to be D&C; full score
paint, molecules: easy 100pt problems
So that'd give me 7th place.
The first solution I got 93pts for in shortcut was this: when checking if the diameter is ≤ D and considering i to be the left endpoint, find the largest j = j1(i) such that a shortcut between i and j gives all distances within the created cycle ≤ D, the largest j = j2(i) such that all distances between vertices from the cycle and vertices to the left of i are ≤ D, then symmetrically for each j the smallest i = i3(j) such that all distances between vertices from the cycle and those to the right of j are ≤ D. There are also distances between pairs of vertices not on the cycle, but those are easy.
For j2(i), we can find the leftmost vertex k2(i) to the right of i such that it's farther from some vertex to the left of i without a shortcut; then, all other vertices on the cycle must be reachable using the shortcut, so pos(j2) - pos(a) + d(a) + C + lft(i) ≤ D for all vertices a between k2 and j2; here, pos is the position of each vertex on the main line (prefix sum of l) and lft(i) is the maximum distance to the left from i; we can extend it to all vertices a to the right of k2, which gives us a bound on pos(j2); we can find j2 by binsearching. Also, k2 can be found using an RMQ table for max(pos+d) and an RMQ-like search.
With j1(i), we can do something similar to finding j2 for each vertex, but only for distances to i exactly, not to the left of i (so there's d(i) instead of lft(i)); j1(i) can be computed as their suffix minima.
We're left with this problem: there's an interval Il(i) and Ir(i) for each i; are there some i, j such that 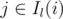 and
and 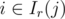 ? This can be solved e.g. using another RMQ table, in which we'll store the minimum left ends of Ir in ranges of j; the right ends of Ir aren't important. Then, for each i, we can find out if the minimum in Il(i) is ≤ i. (Alternatively, we can use a sweepline algorithm and store opened Ir-s in a set<>.)
? This can be solved e.g. using another RMQ table, in which we'll store the minimum left ends of Ir in ranges of j; the right ends of Ir aren't important. Then, for each i, we can find out if the minimum in Il(i) is ≤ i. (Alternatively, we can use a sweepline algorithm and store opened Ir-s in a set<>.)
How simple. /sarcasm
I tried to optimise this, but there was no way to squeeze it even into 97 points — surprisingly, since I didn't really need to optimise to get 93pts.
I got full score on shortcut using an approach based on http://codeforces.com/blog/entry/46518?#comment-310338 (note: extending to all pairs i, j is probably unnecessary and wrong — if i = j, we get a non-path which can be longer than D). The hardest part is computing the smallest j0 = j > i and largest i0 = i < j such that u[i] + v[j] > D, since u[i] and v[j] don't have to be monotonous; afterwards, we can find the smallest/largest sum/difference of x1, x2 by considering all j ≥ j0 / i ≤ i0, for which we only need prefix/suffix maxima of u[] and v[] and check if the answer exists using 2x 2 pointers in O(N).
To compute j0, let's move from i = N - 1 to i = 0 and recompute the sequence of closest increasing v[j]-s using the well-known stack algorithm. Obviously, we can find j0 by binsearching among them, but that gives 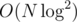 time complexity. However, if j0(i) < j0(i') for i > i', then we can decrease j0(i') to j0(i) without affecting the bounds on the sum/difference of x1, x2; that means we can keep a pointer on the element in the stack (actually an array in the implementation) corresponding to v[j0] and only move this pointer in one direction, giving O(N) complexity.
time complexity. However, if j0(i) < j0(i') for i > i', then we can decrease j0(i') to j0(i) without affecting the bounds on the sum/difference of x1, x2; that means we can keep a pointer on the element in the stack (actually an array in the implementation) corresponding to v[j0] and only move this pointer in one direction, giving O(N) complexity.
This got 97 points instantly, but I still needed some optimisations to get to 100. That time limit was really tight.






