Problem was solved!
Input is consist of 1 ≤ q ≤ 2 * 104 queries every of which are described with single positive integer n not exceeding 4 * 106.
Output is to print for each query: 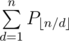
Where:
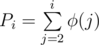
⌊x⌋ = whole part of number, i.e. max integer which's ≤ x
φ(x) is Euler Totient Function
OK, I can previously calculate phis of all numbers from 1 to 4 * 106 and Pi for any i, 1 ≤ i ≤ 4 * 106 in O(nlogn), but what's then? I don't know how to further optimize solution, because it is TLE with O(n) complexity per query.
Please, help me!






