Hello, codeforces!
The community wants so the community gets it! :D Here it is, my very first blog about tasks and algorithms. At the beginning I've decided to post my entries on codeforces, maybe I'll switch to something different if it becomes uncomfortable.
To pour the first blood I decided to choose a task from one of the old ONTAK camps. Task's name is "different words" (you can submit here). The statement goes as follows:
You are given n words (2 ≤ n ≤ 50 000), every of length exactly 5 characters. Each character can be a lowercase letter, an uppercase letter, a digit, a comma... basically, it can be any character with ASCII code between 48 and 122 (let's say that k is the number of possible characters). A task is to find all pairs of indexes of words which are 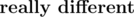 . Two words are
. Two words are 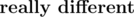 if they differ at all 5 corresponding positions. So for example words
if they differ at all 5 corresponding positions. So for example words 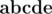 and
and 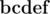 are really different and words
are really different and words 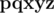 and
and 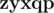 are not, because in both of them the third character is
are not, because in both of them the third character is 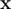 . As there can be many such pairs (up to
. As there can be many such pairs (up to 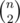 ), if there are more than 100 000 pairs, then the program should print that there are only 100 000 and print this number of pairs (arbitrary chosen).
), if there are more than 100 000 pairs, then the program should print that there are only 100 000 and print this number of pairs (arbitrary chosen).
Please, note that this task comes from the contest which took place a few years ago, so don't think about bitsets. :P
So, how can we attack this problem? At first, you may think about some meet in the middle. It turns out to be hard, even if you can come up with something with k3 in complexity, then it'll probably be multiplied by n. O(k5) is also too much. Inclusion-exclusion principle unfortunately also won't be helpful, as we want to find those pairs, not only count them, and working on sets of words won't be so effective.
The biggest problem is that k is big. If it'd be, let's say, up to 10, then it'd be solvable in some way, but I won't go deeply into this solution, cause it isn't interesting and k is of course bigger. But I've mentioned small k. Why couldn't we dream about even smaller k? If k would be up to 2 (so words would consist only of digits 0 and 1) then this task would be trivial. We'd just group words which are the same, and for each word its set of really different words would be the group with words where every zero is changed into one and vice versa. But again, k isn't small...
Buuuuut, we can imagine that it is! Let's say that we assume that characters with even ASCII characters are "new zeros" and characters with odd ASCII characters are "new ones". Then for sure if two words are really different with these assumptions, then they are really different without them, cause if they'd have this same character at some position, then this character would change into this same "new character". This allows us to find some pairs, unfortunately not all of them, but the way definitely looks encouragingly.
If we've found some of the pairs, maybe we should just try one more time? But how should we change characters now? Now comes an experience: if you have no idea what to do or you don't want to do some complicated construction, then just do something random! So we could randomly change every character into zero or one and then run our algorithm for k equal to 2 — match groups of opposite words. What's the probability for a fixed pair that we'd find it during one run of our algorithm? If we already know what we've assigned to each character of the first word, then on every corresponding position in the second word there should be a different character — for each position we have a  chance, that this assigned character will be correct, so we have probability equal to
chance, that this assigned character will be correct, so we have probability equal to 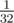 that the whole word will match.
that the whole word will match.
What's the number of needed runs? Looking at limits we can guess that it could be a few hundred. Let's calculate the probability of fail if we'd repeat algorithm 600 times. The probability that we wouldn't find some pair is equal to 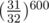 , the probability that we'd find it,
, the probability that we'd find it, 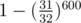 of course, and finally, the probability that we'd find all of them (or some 100 000 of them) is equal to
of course, and finally, the probability that we'd find all of them (or some 100 000 of them) is equal to 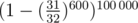 which is greater than 0.999, so it's definitely enough.
which is greater than 0.999, so it's definitely enough.
There is one more thing. Consider words 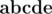 and
and 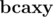 . They are really different. Let's say that we've assigned 0 to a. Then we have to assign 1 to b. Then we have to assign 0 to c. Then we have to assign 1 to a. So there is a problem... At first glance, it might look problematic, but it turns out that it's easy to fix it. We shouldn't just assign zeros and ones to characters. We should assign them to pairs (character, position). Then everything will go well.
. They are really different. Let's say that we've assigned 0 to a. Then we have to assign 1 to b. Then we have to assign 0 to c. Then we have to assign 1 to a. So there is a problem... At first glance, it might look problematic, but it turns out that it's easy to fix it. We shouldn't just assign zeros and ones to characters. We should assign them to pairs (character, position). Then everything will go well.
Total complexity is something like O(n·600·log(n)), but we can get rid of the log factor by using hashmaps.
Sooooo, it's the end of my first blog, sorry if it's too long. I hope that you've found this task useful and interesting. What do you think about this format, what was missing, what was bad? It'd be great to see a feedback from you. See you next time! :D






