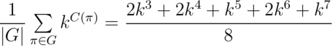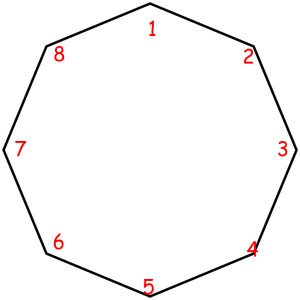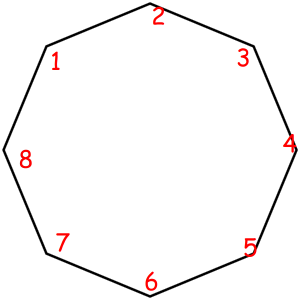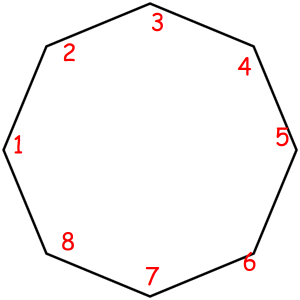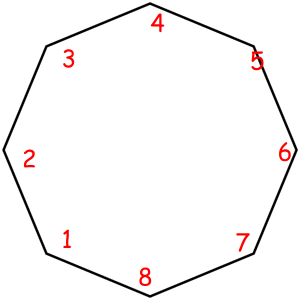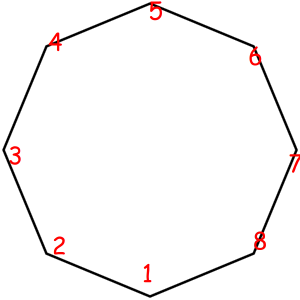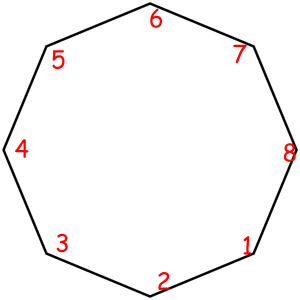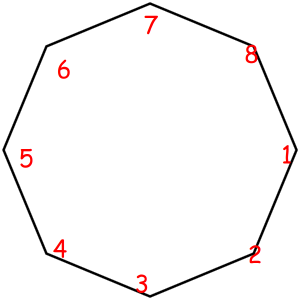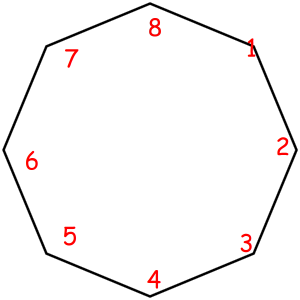
Consider some object that can be represented as a sequence of something with some magic property. Magic property means we consider two such objects equal if one object can be obtained from another using some given permutation. For example, look at these equal necklaces of 8 elements with magic property "we consider two necklaces equal if one can be obtained from another with rotating":
The corresponded special permutations are: 12345678, 23456781, 34567812, 45678123, 56781234, 67812345, 78123456, 81234567
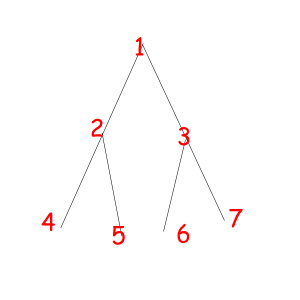
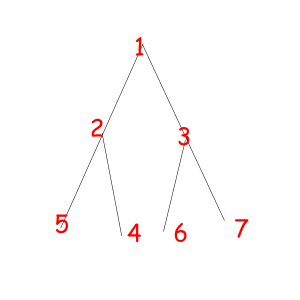
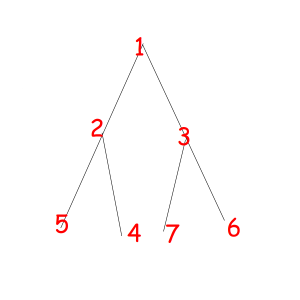
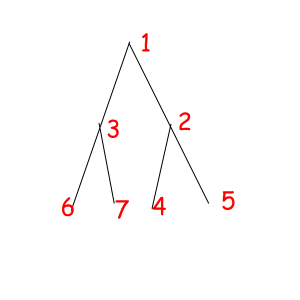
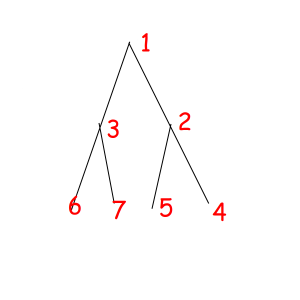
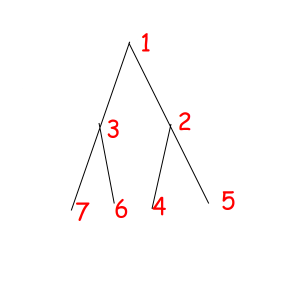
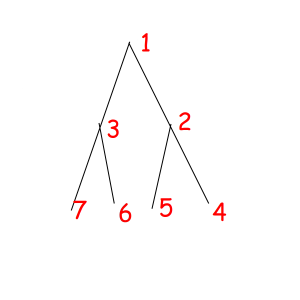
Or look at these equal binary trees of size 7 with a magic property "we consider two trees equal if we can obtain one from another with permuting children of some vertexes":
The corresponded special permutations are: 1234567, 1234576, 1235467, 1235476, 1326745, 1326754, 1327645, 1327654.
Now we are given a problem: we have such an object with a magic property, and in how many ways we can paint elements of its sequence in k colours if we count equal paintings as one? According to burnside's lemma for this case, the answer is 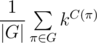 , where G is the set of special permutations, C(π) is the number of cycles in permutation π.
, where G is the set of special permutations, C(π) is the number of cycles in permutation π.
Let's try to solve this problem for reviewed binary tree with 7 vertexes:
G = (1234567, 1234576, 1235467, 1235476, 1326745, 1326754, 1327645, 1327654)
C(1234567) = 7: 1, 2, 3, 4, 5, 6, 7
C(1234576) = 6: 1, 2, 3, 4, 5, 6 - 7
C(1235467) = 6: 1, 2, 3, 4 - 5, 6, 7
C(1235476) = 5: 1, 2, 3, 4 - 5, 6 - 7
C(1326745) = 4: 1, 2 - 3, 4 - 6, 5 - 7
C(1326754) = 3: 1, 2 - 3, 4 - 6 - 5 - 7
C(1327645) = 3: 1, 2 - 3, 4 - 7 - 5 - 6
C(1327654) = 4: 1, 2 - 3, 4 - 7, 5 - 6
So the answer is