In various places(1, 2, ), people have talked about "Dinic's With Scaling" having $$$O(VElog(U))$$$ complexity, where U is the max edge capacity. However, in just as many places, people have cast doubt about this complexity or worried that this algorithm ends up being slower in practice(12.
I had the same doubts. In fact, a couple months ago I benchmarked Dinic's with scaling on some hard test cases and thought that Dinic's with/without scaling performed similarly.
As it turns out, I benchmarked it again yesterday and found that Dinic's with scaling definitely has significantly better asymptotic complexity (by a factor of V).
Synthetic Benchmarking
I used the hard test case generator at 2 posted by ko_osaga here. The one posted at 1 creates a graph with only V edges and moreover, doesn't work for me... Notably, given a V, it generates a graph with V nodes and $$$O(V^2)$$$ edges.
The code I used was my own Dinic's implementation (originally from emaxx) found here. Notably, the SCALING variable toggles between Dinic's with scaling and without. It's a small change, as you can see.
I ran the two code across a variety of input sizes, averaging across 10 runs, then taking the log of input size and times, plotting them in a 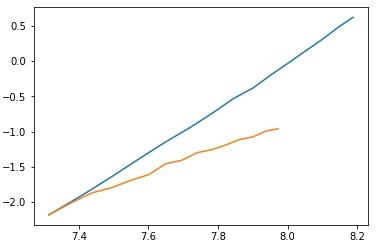 where blue is the runtime of Dinic's without scaling and orange is the runtime of Dinic's with scaling. Since the important thing to look at is the slope of the line, I normalized the lines to start at the same point.
where blue is the runtime of Dinic's without scaling and orange is the runtime of Dinic's with scaling. Since the important thing to look at is the slope of the line, I normalized the lines to start at the same point.
Fitting a linear regression to the points, we see that the slope of Dinic's without scaling is 3.204, while the slope of Dinic's with scaling is 1.93, which correspond to complexities of $$$O(V^3)$$$ and $$$O(V^2)$$$ respectively.
In terms of actual runtime, here are some numbers on specific sizes.
Benchmarking on Problems
There are 3 flow problems, I benchmarked on — SPOJ FASTFLOW, (VNSPOJ FASTFLOW)[https://vn.spoj.com/problems/FFLOW/), and a Chinese LOJ Flow Problem (it's intended to solve this problem with Highest Label Preflow Push, which has $$$O(V^2\sqrt{E})$$$ complexity).
Also, to vouch for the superiority of my solution, here's some benchmarks with other implementations :^) Mine (to enable scaling change the SCALING boolean), Emaxxs dinic, LOJ fastest (the fastest submission on the Chinese flow problem).
SPOJ (V<=5000, E<=3e4)
Mine: 0.04
Emaxx Dinic: 0.11
Mine w/ scaling: 0.27
VNSPOJ (V<=5000, E<=3e4, harder test cases):
Mine: TLE
Emaxx dinic: TLE
Mine w/ scaling: 0.00
LOJ (V<=1200, E<=120000):
Mine: 56 points
Mine w/ scaling: 88 points
Emaxx dinic: 44 points
Synthetic Test(N=2000, E=4e6):
Mine: 66.56
Emaxx dinic: 247.40
Mine w/ scaling: 0.14 LOJ fastest:





