Thanks everybody for participating. Tasks follow in the order of the original contest (the mirror order is given in the brackets).
562A - Logistical Questions
(in mirror: 566C - Logistical Questions)
Let's think about formal statement of the problem. We are given a tricky definition of a distance on the tre: ρ(a, b) = dist(a, b)1.5. Each vertex has its weight wi. We need to choose a place x for a competition such that the sum of distances from all vertices of the tree with their weights is minimum possible: f(x) = w1ρ(1, x) + w2ρ(x, 2) + ... + wnρ(x, n).
Let's understand how function f(x) works. Allow yourself to put point x not only in vertices of the tree, but also in any point inside each edge by naturally expanding the distance definition (for example, the middle of the edge of length 4 km is located 2 km from both ends of this edge).
Fact 1. For any path 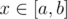 in the tree the function ρ(i, x) is convex. Actually, the function dist(i, x) plot on each path [a, b] looks like the plot of a function abs(x): it first decreases linearly to the minimum: the closes to i point on a segment [a, b], and then increases linearly. Taking a composition with a convex increasing function t1.5, as we can see, we get the convex function on any path in the tree. Here by function on the path we understand usual function of a real variable x that is identified with its location on path x: dist(a, x). So, each of the summands in the definition of f(x) is convex on any path in the tree, so f(x) is also convex on any path in the tree.
in the tree the function ρ(i, x) is convex. Actually, the function dist(i, x) plot on each path [a, b] looks like the plot of a function abs(x): it first decreases linearly to the minimum: the closes to i point on a segment [a, b], and then increases linearly. Taking a composition with a convex increasing function t1.5, as we can see, we get the convex function on any path in the tree. Here by function on the path we understand usual function of a real variable x that is identified with its location on path x: dist(a, x). So, each of the summands in the definition of f(x) is convex on any path in the tree, so f(x) is also convex on any path in the tree.
Let's call convex functions on any path in the tree convex on tree. Let's formulate few facts about convex functions on trees.
Fact 2. A convex function on tree can't have two different local minimums. Indeed, otherwise the path between those minimums contradicts the property of being convex on any path in the tree.
So, any convex function f(x) on the tree has the only local minimum that coincides with its global minimum.
Fact 3. From each vertex v there exists no more than one edge in which direction the function f decreases. Indeed, otherwise the path connecting two edges of function decrease would contradict the definition of a convex function in a point v.
Let's call such edge that function decreases along this edge to be a gradient of function f in point x. By using facts 2 and 3 we see that in each vertex there is either a uniquely defined gradient or the vertex is a global minimum.
Suppose we are able to efficiently find a gradient direction by using some algorithm for a given vertex v. If our tree was a bamboo then the task would be a usual convex function minimization that is efficiently solved by a binary search, i. e. dichotomy. We need some equivalent of a dichotomy for a tree. What is it?
Let's use centroid decmoposition! Indeed, let's take a tree center (i. e. such vertex that sizes of all its subtrees are no larger than n / 2). By using fact 3 we may consider the gradient of f in the center of the tree. First of all, there may be no gradient in this point meaning that we already found an optimum. Otherwise we know that global minimum is located in a subtree in direction of gradient, so all remaining subtrees and the center can be excluded from our consideration. So, by running one gradient calculation we reduced the number of vertices in a considered part of a tree twice.
So, in  runs of gradient calculation we almost solved the problem. Let's understand where exactly the answer is located. Note that the global optimum will most probably be located inside some edge. It is easy to see that the optimum vertex will be one of the vertices incident to that edge, or more specifically, one of the last two considered vertices by our algorithms. Which exactly can be determined by calculating the exact answer for them and choosing the most optimal among them.
runs of gradient calculation we almost solved the problem. Let's understand where exactly the answer is located. Note that the global optimum will most probably be located inside some edge. It is easy to see that the optimum vertex will be one of the vertices incident to that edge, or more specifically, one of the last two considered vertices by our algorithms. Which exactly can be determined by calculating the exact answer for them and choosing the most optimal among them.
Now let's calculate the gradient direction in a vertex v. Fix a subtree ui of a vertex v. Consider a derivative of all summands from that subtree when we move into that subtree. Denote this derivative as deri. Then, as we can see, the derivative of f(x) while moving from x = v in direction of subtree ui is - der1 - der2 - ... - deri - 1 + deri - deri + 1 - ... - derk where k is a degree of vertex v. So, by running one DFS from vertex v we may calculate all values deri, and so we may find a gradient direction by applying the formula above and considering a direction with negative derivative.
Finally, we got a solution in  .
.
562B - Clique in the Divisibility Graph
(in mirror: 566F - Clique in the Divisibility Graph)
Order numbers in the sought clique in ascending order. Note that set X = {x1, ..., xk} is a clique iff 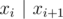 for (1 ≤ i ≤ k - 1). So, it's easy to formulate a dynamic programming problem: D[x] is equal to the length of a longest suitable increasing subsequence ending in a number x. The calculation formula:
for (1 ≤ i ≤ k - 1). So, it's easy to formulate a dynamic programming problem: D[x] is equal to the length of a longest suitable increasing subsequence ending in a number x. The calculation formula: 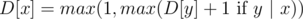 for all x in set A.
for all x in set A.
If DP is written in "forward" direction then it's easy to estimate the complexity of a solution. In the worst case we'll process 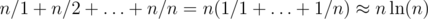 transitions.
transitions.
562C - Restoring Map
(in mirror: 566E - Restoring Map)
Let's call a neighborhood of a vertex — the set consisting of it and all vertices near to it. So, we know the set of all neighborhoods of all vertices in some arbitrary order, and also each neighborhood is shuffled in an arbitrary order.
Let's call the tree vertex to be internal if it is not a tree leaf. Similarly, let's call a tree edge to be internal if it connects two internal vertices. An nice observation is that if two neighborhoods intersect exactly by two elements a and b then a and b have to be connected with an edge, in particular the edge (a, b) is internal. Conversely, any internal edge (a, b) may be represented as an intersection of some two neighborhoods С and D of some two vertices c and d such that there is a path c – a – b – d in the tree. In such manner we may find all internal edges by considering pairwise intersections of all neighborhoods. This can be done in about n3 / 2 operations naively, or in 32 times faster, by using bitsets technique.
Note that knowing all internal edges we may determine all internal vertices except the only case of a star graph (i. e. the graph consisting of a vertex with several other vertices attached to it). The case of a star should be considered separately.
Now we know the set of all leaves, all internal vertices and a tree structure on all internal vertices. The only thing that remained is to determine for each leaf, to what internal vertex is should be attached. This can be done in following manner. Consider a leaf l. Consider all neighborhoods containing it. Consider a minimal neighborhood among them; it can be shown that it is exactly the neighborhood L corresponding to a leaf l itself. Consider all internal vertices in L. There can be no less than two of them.
If there are three of them or more then we can uniquely determine to which of them l should be attached — it should be such vertex from them that has a degree inside L larger than 1. If there are exactly two internal vertices in L (let's say, a and b), then determining the attach point for l is a bit harder.
Statement: l should be attached to that vertex among a, b, that has an internal degree exactly 1. Indeed, if l was attached to a vertex with internal degree larger than 1, we would have considered this case before.
If both of vertices a and b have internal degree — 1 then our graph looks like a dumbbell (an edge (a, b) and all remaining vertices attached either to a or to b). Such case should also be considered separately.
The solution for two special cases remains for a reader as an easy exercise.
562D - Restructuring Company
(in mirror: 566D - Restructuring Company)
This problem allows a lot of solution with different time asymptotic. Let's describe a solution in 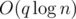 .
.
Let's first consider a problem with only a queries of second and third type. It can be solved in a following manner. Consider a line consisting of all employees from 1 to n. An observation: any department looks like a contiguous segment of workers. Let's keep those segments in any logarithmic data structure like a balanced binary search tree (std::set or TreeSet). When merging departments from x to y, just extract all segments that are in the range [x, y] and merge them. For answering a query of the third type just check if employees x and y belong to the same segment. In such manner we get a solution of an easier problem in  per query.
per query.
When adding the queries of a first type we in fact allow some segments to correspond to the same department. Let's add a DSU for handling equivalence classes of segments. Now the query of the first type is just using merge inside DSU for departments which x and y belong to. Also for queries of the second type it's important not to forget to call merge from all extracted segments.
So we get a solution in 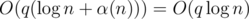 time.
time.
562E - Max and Min
(in mirror: 566G - Max and Min)
Consider a following geometrical interpretation. Both Max and Min have a set of vectors from the first plane quadrant and a point (x, y). During his turn Max may add any of his vectors to a point (x, y), and Min — may subtract any of his vectors. Min wants point (x, y) to be strictly in the third quadrant, Max tries to prevent his from doing it. Denote Max vectors as Mxi and Min vectors as Mnj.
Consider a following obvious sufficient condition for Max to win. Consider some non-negative direction in a plane, i. e. such vector (a, b) that a, b ≥ 0 and at least one of numbers a, b is not a zero. Then if among Max vectors there is such vector Mxi, that it's not shorter than any of Min vectors Mnj along the direction (a, b) then Max can surely win. Here by the length of vector v along a direction (a, b) we mean a scalar product of vector v and vector (a, b).
Indeed, let Max always use that vector Mxi. Then during the turns of Max and Min point (x, y) is shifted by a vector Mxi - Mnj for some j, so its overall shift along the vector (a, b) is equal to ((Mxi - Mnj), (a, b)) = (Mxi, (a, b)) - (Mnj, (a, b)) ≥ 0. By observing that initially the scalar produt ((x, y), (a, b)) = ax + by > 0 we see that at any moment ax + by will be strictly positive. This means that Min won't be able at any moment to make x and y both be negative (since it would mean that ax + by < 0).
Now let's formulate some kind of converse statement. Suppose Max vector Mxi lies strictly inside the triangle formed by Min vectors Mnj and Mnk. In particular, vector Mxi endpoint can't lie on a segment [Mnj, Mnk], but it may be collinear one of vectors Mnj and Mnk.
Note that since Mxi lies strictly inside the triangle formed by vectors Mnj and Mnk it can be extended to a vector Mx'i, whose endpoint lies on a segment [Mnj, Mnk]. By using linear dependence of Mx'i and Mnj, Mnk we have that Mx'i = (p / r)Mnj + (q / r)Mnk, where p + q = r and p, q, r — integer non-negative numbers. This is equivalent to a formula rMx'i = pMnj + qMnk. This means that if per each r turns of Max in Mxi we will respond with p turns of Min in Mnj and q turns of Min in Mnk, then the total shift will be equal to - pMnj - qMnk + rMxi = - rMx'i + rMxi = - r(Mx'i - Mxi), that is the vector with strictly negative components. So, we are able to block that Max turn, i. e. it does not give any advantage to Max.
The natural wish is to create a convex hull of all Min turns and to consider all Max turns in respect to it. If Max turn lies inside the convex hull of Min turns, then by using the previous fact this turn is meaningless to Max. Otherwise, there are two possibilities.
First, this turn may intersect the hull but go out of it somewhere; in this case this Max turn is no shorter than all Min turns in some non-negative direction (more specifically, in its own direction), so Max wins.
On the other hand, Max vector lies to aside from the Min turns convex hull. Let's suppose the vector Mxi lies to the left of the Min turns. This case requires a special analysis. Consider the topmost of the Min vectors Mnj. If Mxi is no lower than Mxj, then by using the first fact Max is able to win by using only this vector. Otherwise the difference Mni - Mxj is a vector with strictly negative components, by using which we are able to block that Max vector.
So, the full version of a criteria for Min being a winner looks like the following. Consider a convex hull of Min turns and expand it to the left of the topmost point and to the bottom of the rightmost point. If all Max turns lie strictly inside the formed figure then Min wins, otherwise Max wins.
562F - Matching Names
(в трансляции: 566A - Matching Names)
Form a trie from all names and pseudonyms. Mark with red all vertices corresponding to names, and with blue all vertices corresponding to the pseudonyms (a single vertex may be marked several times, possibly with different colors). Note that if we match a name a and a pseudonym b, then the quality of such match is lcp(a, b) = 1 / 2(2 * lcp(a, b)) = 1 / 2(|a| + |b| - (|a| - lcp(a, b)) - (|b| - lcp(a, b))), that is equal to a constant 1 / 2(|a| + |b|), with subtracted half of a length of a path between a and b over the trie. So, what we need is to connect all red vertices with blue vertices with paths of a minimum possible total length.
This can be done with a following greedy procedure: if we have a vertex v with x red vertices and y blue vertices in its subtree then we must match min(x, y) red vertices of its subtree to min(x, y) blue vertices of its subtree and leave the remaining max(x, y) - min(x, y) ref or blue vertices to the level higher. The correctness of such algorithm may be easily shown by the next idea. Give each edge of each path a direction from a red vertex to a blue. If some edge recieves two different directions after this procedure, we may cross-change two paths through it so that their total length is reduced by two.
So, we get a solution in O(sumlen) where sumlen is a total length of all names and pseudonyms.
562G - Replicating Processes
(в трансляции: 566B - Replicating Processes)
==== UNTRANSLATED SECTION, PLEASE WAIT A FEW MINUTES... ====

Kitten to take your attention :)
This problem may be solved by simulating the replication process. Let's keep a list of all replications that may be applied by the current step. Apply an arbitrary replication, after that update a list by adding/removing all suitable or now unsuitable replications touching all affected on current step servers. The list of replications may be kept in a "double-linked list" data structure, that allows to add and remove elements to/from the set and to extract an arbitrary element of the set in O(1).
The proof of correctness of such algorithm is not hard and is left as an exercies (maybe it will appear here later).
We got a solution in O(n) operation (though, the constant hidden by O-notation is pretty large; the input size is already 12n numbers and the solution itself hides a constant 36 or higher).






























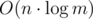 .
.
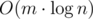 .
.


