It is well known that length of Longest Alternating Subsequence can be found in O(n) (Hint: Think graphically).
My question is can we count the number of Longest Alternating Subsequences in a List in O(n).
As an example consider: A[6]=[2 4 1 3 4 2]
where LAS would be 5, and there are 3 such subsequences.










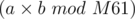 , where a and b can both have at most 61 bits.
, where a and b can both have at most 61 bits.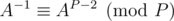 ?
?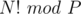 for prime P
for prime P

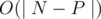 doesnt pass!
doesnt pass! 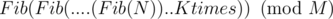

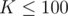 and same constrains on
and same constrains on 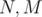
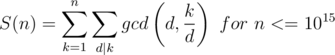
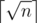 .
.
