The problem can be found here: https://onlinejudge.org/index.php?option=com_onlinejudge&Itemid=8&page=show_problem&problem=4878
| # | User | Rating |
|---|---|---|
| 1 | ecnerwala | 3649 |
| 2 | Benq | 3581 |
| 3 | orzdevinwang | 3570 |
| 4 | Geothermal | 3569 |
| 4 | cnnfls_csy | 3569 |
| 6 | tourist | 3565 |
| 7 | maroonrk | 3531 |
| 8 | Radewoosh | 3521 |
| 9 | Um_nik | 3482 |
| 10 | jiangly | 3468 |
| # | User | Contrib. |
|---|---|---|
| 1 | maomao90 | 174 |
| 2 | awoo | 164 |
| 3 | adamant | 162 |
| 4 | TheScrasse | 159 |
| 5 | nor | 158 |
| 6 | maroonrk | 156 |
| 7 | -is-this-fft- | 151 |
| 8 | SecondThread | 147 |
| 9 | orz | 146 |
| 10 | pajenegod | 145 |
Hello,
I was implementing a simple Trie when I found a behavior that I didn't understand. I followed the program using a debugger, the issue seems to be in the insert function. I explained the issue in code comments.
struct Trie{
struct Node{
int id, nxt[26];
Node(int id) : id(id)
{
memset(nxt, -1, sizeof(nxt));
}
};
vector<Node> v;
vector<bool> leaf;
void init()
{
v.clear();
leaf.clear();
addNode();
}
int addNode()
{
v.push_back(v.size());
leaf.push_back(false);
return (int)(v.size()) - 1;
}
int getSizeMinusOne()
{
return (int)(v.size()) - 1;
}
void insert(const string &s)
{
int cur = 0;
for (char c : s)
{
c -= 'a';
if (v[cur].nxt[c] == -1)
{
// Note I only use one of the following NOT both at the same time
// Approach (1)
// v[cur].nxt[c] doesn't get updated. Stays -1 and RTEs later on due to out of boundary access
v[cur].nxt[c] = addNode();
// Approach (2)
// works fine
addNode();
v[cur].nxt[c] = getSizeMinusOne();
}
cur = v[cur].nxt[c];
}
leaf[cur] = true;
}
};
I also found out that both approaches seem to work find when changing the array nxt to a vector instead of an array. Could someone explain why this happens when nxt is an array? And why approach (2) works fine even if nxt is an array?
Hello,
Here is the problem: https://codingcompetitions.withgoogle.com/kickstart/round/000000000019ff48/00000000003f4dea
Here is my solution: https://ideone.com/pazUnT It passed the first testset successfully.
My solution is a simple DP with 2 parameters.
$$$have$$$ is a vector of size $$$M$$$. $$$have[j]$$$ contains the number of times die face $$$j$$$ has been locked in previous rolls.
$$$dp[i][have]$$$ is the expected number of rolls (When rolling optimally) to create the desired $$$K$$$ groups from dice $$$i...n$$$ having previous rolls represented in $$$have$$$.
What I need help with is the 'rolling optimally' part. I assumed that we will only reroll a die iff the resulting configuration (represented in $$$have$$$ vector) can not possibly create the desired $$$K$$$ groups no matter how we roll the rest of the dice. Otherwise, we will keep our roll and move on to the next die.
How do we prove that it is never optimal to reroll when we have a configuration that can reach an answer?
My attempt was the following:
let $$$E(s)$$$ represent the answer for state $$$s$$$, and $$$R(s)$$$ represents the expected number of rerolls we need to get state $$$s$$$ from our current state.
let $$$a, b$$$ both be valid states that we can reach from our current state. Both $$$a, b$$$ can reach an answer. And $$$E(a) < E(b)$$$.
It is optimal to reroll after reaching state $$$b$$$ iff $$$E(a) + R(a) \leq E(b)$$$.
$$$R(a)$$$ is actually equal to $$$M$$$ since next state is defined only by what die face we get. The probability to get any face is $$$1/M$$$ and the expected value is $$$M$$$. So we it's optimal to keep rerolling iff $$$E(b) - E(a) \geq M$$$.
I have failed to progress any further and I don't even know if that approach is even correct. I think my proof attempt is missing a sort of a case where we're not targeting a specific die face but considering rerolling until we reach one of several die faces or reach a number of rerolls. Please correct me or tell me another approach.
Thanks.
Since everyone's sharing their journeys in cp, I thought I might as well. Hope you don't find it relatable. Here is the timeline of my journey.
- Got exposed to programming when I was a kid. Had all the resources and guidance I needed to start. Doing nothing was much more appealing back then.
- Reach 18. Have to pick something to study in college. Everyone is studying cs nowadays so why not jump on the bandwagon? I sit in front of a screen all day anyway so this will fit me, right?
- It didn't.
- Hear that big companies that have sleeping capsules and free food ask algorithmic questions in their interviews.
- Start solving problems.
- It's not like anything else is remotely interesting. Everything is built above nine thousand layers of abstraction it's fucking impossible to understand shit. Would much rather if people explained stuff in core instead of giving tricks on the surface to memorize to get shit done.
- Keep solving problems to escape the guilt that i'm doing nothing useful.
- Addicted to competitions anyway since it's the only source of validation for my fragile ego.
- Took 3 years for rating inflation to finally happen.
- ???
- Share my story and get downvoted to hell but it's not like it matters anyway.
Edit: I was pointed out that this might be demotivating for some. Please note that most of this has been exaggerated for satire purposes (sorry if you were relating up to this point :c). I just wanted to poke these recent blog posts of people having a rate increase in no time.
I've been learning about Aliens dp trick from here: http://serbanology.com/show_article.php?art=The%20Trick%20From%20Aliens and I had a few doubts about it.
1- In the pseudocode section in the blog. If we're solving the problem for exactly $$$k$$$ instead of less than or equal to $$$k$$$, will we have to include negative penalty values in the binary search range as we might need to move in both directions of the optimum point?
2- Regarding the reconstruction issues section.
What I've understood (kinda) is that if our function is not strictly convex (i.e. might look something like the image below), No penalty value will ever get us a value between $$$a$$$, and $$$b$$$. I've also understood that if our binary search could get us $$$a$$$ (Our best effort for the greatest value less than or equal to $$$k$$$), then $$$ans[k] = ans[a] + (k - a) * t$$$ where $$$t$$$ is the step of the arithmetic progression (Since the function is linear between $$$a$$$, and $$$b$$$). I don't understand how we reached $$$ans[k] = ans[a] - (k - a) * penaltyValue$$$ from that. (The equations in the blog are using $$$p$$$ instead of $$$a$$$).

Hello,
I was trying to solve 383E - Vowels. Using the technique described here: https://codeforces.com/blog/entry/45223
I managed to get AC here: 61233188 using regular memory reduction (Reducing one of the dimensions to the size of 2).
I don't understand how it can be reduced to one-dimensional like this: 61233599.
Here is an image (with my amazing paint skills :P) to demonstrate my understanding of the dp dependencies in this problem: 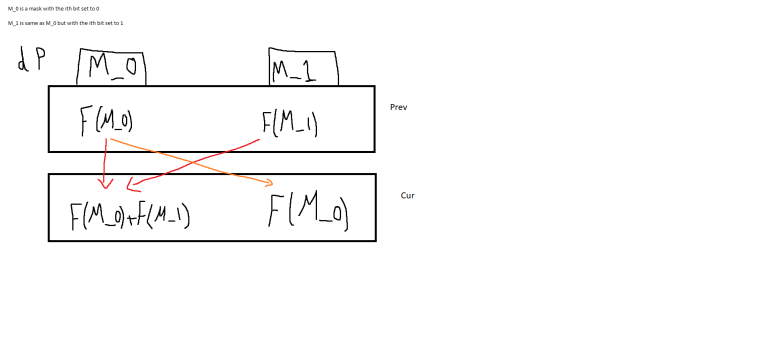
I can't see how these updates are done in the solution with only one dimension.
Any help would be appreciated.
Thanks.
Hello,
I have been trying solving this problem: 1747 — Swap Space
Here is my WA code: https://ideone.com/64kU5M
I think the issue is with my comparator since I've seen solutions with other comparators that get AC like this one: https://github.com/morris821028/UVa/blob/master/volume017/1747%20-%20Swap%20Space.cpp
The idea behind my comparator is: if there are 2 disks to be reformatted $$$X$$$ and $$$Y$$$ and I have available storage $$$S$$$. Then if I take $$$X$$$ before $$$Y$$$
$$$S$$$ must be >= $$$X.A$$$ and $$$S + X.B - X.A$$$ >= $$$Y.A$$$, with rearragement:
$$$S >= max(X.A, Y.A - X.B + X.A)$$$
Similarly if i take $$$Y$$$ before $$$X$$$
$$$S >= max(Y.A, X.A - Y.B + Y.A)$$$
thus my comparator between $$$X$$$ and $$$Y$$$ is like this
bool cmp(pair<long long, long long> x, pair<long long, long long> y)
{
return max(x.first, x.first + y.first - x.second) < max(y.first, x.first + y.first - y.second);
}
Could somebody tell me what's wrong with my comparator?
Thanks.
Hello,
I was trying to solve 1117D - Magic Gems using Matrix Exponentiation. I'm trying to use an implementation (It was moriss821028's if I recall correctly) for Matrix Power since it's much faster than mine. I'm using 2 transformation matrices and multiply them to get the final transformation matrix named transform and then raise it to the power of n.
This submission: 58207232 gets AC, while on my machine it gives segmentation fault on line: 108, the line where I raise the transform matrix to the power of n. Following it with the debugger, it doesn't enter the operator ^ function at all, it stops on the definition line and halts.
Reducing the dimensions of the array v to 180 x 180 seems to fix the issue locally but the code doesn't seem to take that much memory. Idk if this is related to a memory leak or what.
My IDE is CLion, the compiler is MinGW version 5.0, my CMake version is 3.13.2, and I'm using C++ 14.
It prints exit message Process finished with exit code -1073741571 (0xC00000FD).
If there is any more information you need, please ask. I'm a kind of a newbie when it comes to these stuff.
Any help would be appreciated
Hi,
AC Code (2.5s): 56017075 (Or here if you can't view gym submissions)
TLE (over 30s, tested on custom private group contest with custom TL): 56017081 (Or here)
Regardless of the problem and its solution, the ONLY line that changes between the 2 submissions is the way I check if the state was calculated before or not. When I check it using if (ret != -1) it gives TLE, but when I check it using visit array is (visit[i][j] == vid) it passes. I don't even remove the extra memset for memoization array in each testcase when using the visit array. Why would this very small change result in that huge difference in time?
Hello,
In problem: 233B - Non-square Equation
I was wondering why in submissions like this 12604154 it is sufficient to only check a small range around the square root of n. How can I deduct something like this from the equation, and how to prove it?
Thanks.
Update: Here's a formulation that helped me understand it, maybe it'll be useful for someone.
The main equation is: $$$X^2 + X * S(X) = N$$$
Let $$$Y = X + S(X)$$$.
$$$Y^2 = X^2 + 2 * X * S(X) + {(S(X))}^2$$$ $$$Thus$$$
$$$Y^2 >= X^2 + X * S(X)$$$
Since $$$X^2 + X * S(X) = N$$$ then
$$$Y^2 >= N$$$
$$${(X + S(X))}^2 >= N$$$
$$$X + S(X) >= sqrt(N)$$$
$$$X >= sqrt(N) - S(X)$$$
Also, check mohamedeltair's comment for a general proof for the upper bound.
Hello,
Here's the problem link: https://uva.onlinejudge.org/index.php?option=com_onlinejudge&Itemid=8&page=show_problem&problem=1159
I know and already got AC with other neater solutions, but I was trying various dp states/approaches for practice. I wanted to know what I am missing in this dp approach since I'm getting a bit lower value than the sample output (0.5012511 instead of 0.5002286)
Solution link: https://ideone.com/AjdoVF
approach:
- i is zero based
Dp definition:
- dp[i][rem] is probability to get a final even 'usedCandy' count in range [i, m) using 'rem' candies such that usedCandy = totalCandies — rem
base case:
- at i == m, return isEven(usedCandy)
transition:
at each [i][rem], if 'tk' is amount given to man 'i'. 'tk' is in [0, rem]
answer = Summation for all 'tk' in [0, rem] -> P(man 'i' getting exactly tk candies) * dp[i + 1][rem — tk]
P(a man getting exactly 'tk' candies) having 'rem' candies in total can be found through binomial theorom C[rem][tk] * p^tk q^(rem — tk) such that p is probability for
a person to get a single candy = 1/(m+w) and q = 1 — p
If something is not clear with my solution, please ask. Where am I going wrong with this dp?
Here's the problem : 227C - Flying Saucer Segments
In the editorial here: http://codeforces.com/blog/entry/5378?locale=en We ended up having F(n) = 3*(F(n-1) + 1) — 1 Could somebody please elaborate on how to get we got ((3^n) — 1) from the recurrence? Sorry if this is a newbie question I'm trying to learn more on the topic.
http://codeforces.com/blog/entry/14256 in D2-C.
I understood that for each x there is exactly 1 k. But how can I prove that for each K in [1, a] there always exists nice numbers for all remainders [1, b-1]? For instance if a = 3, b = 5. How to be so sure that for Each k {1, 2, 3} there will always be nice numbers with remainder values [1, b-1]
| Name |
|---|










