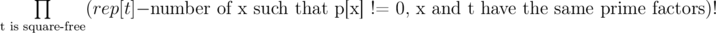Hello everybody, this time I just want to share the situation that I lived yesterday during the round 422. I like math problems, so I decided to start solving problem D(I solved the problem and got pretest passed with 1430 ~ 1450 ms(I don't remember exactly) since I submitted an nlogn solution). Well, at that moment, I was aware that the final verdict in the System Test could be TLE, however, my solution during the contest should take the same time for any input since I precomputed the value of the prefix sums and, right after that, the output can be found substracting and multiplying some variables.
Thus, I thought that if that solution had passed pretest, it must pass the SysTest as well(even when it was slow). Okay, after some time, the contest ended and the SysTest started. I was waiting for my submission for problem D and I noticed that, on the status page, my submission got TLE on test 1 and suddenly, it disappeared from the standings. As you can see, it seems that I never submitted any solution for D.
At that moment, I was a bit confused by the situtation and I sent messages to the author contest Melnik and to the coordinators of the contest. Well, after some time, the ratings were updated D: and I didn't receive any answer from them. After some more minutes, Melnik replied to my message. He explained that it was unexpected and he was really sorry about it(I understand that there are always some issues during any contest).
I decided to forget that situation yesterday. Today, with a better mood, I decided to submit exactly the same solution again(was it really TLE on test 1? Hahaha) and the result was this (The answer was: No, it seems it was not TLE on test1).
It turned out to be really sad because I would rank around 20 — 30(and I would have recovered my violet color) instead of ranking 420 :D and decrease my rating by 30. Moreover, according to the Editorial the first submission for D in Div2 was after 18 minutes while mine was in 17 minutes. Totally sad.
Okay, that was my sad story(maybe in some other contest I can still recover my violet color) and as Len pointed out, I was relying on my luck too much.
However, currently, I ask the same thing that sup_bro asked in the comments. Why does Codeforces run our code against pretest again? For instance, if they had run my solution against the first official test(those that don't belong to the pretest), this situtation wouldn't have occurred. I think that the answer to this question can be something technical that almost doesn't mind in competitive programming, but I would like to read some answer just to feel a bit better.









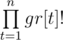 .( Note that above we were considering the array p was empty, so if p has some entries already assigned, say
.( Note that above we were considering the array p was empty, so if p has some entries already assigned, say  then the only group with the same numbers of
then the only group with the same numbers of 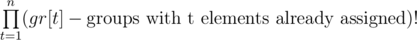
 . (Here we don't have to deal with the verification in which some values of p are already assigned because we already did the verification before(assigment bettwen indexes) i.e. if x and y have the same prime factors, then
. (Here we don't have to deal with the verification in which some values of p are already assigned because we already did the verification before(assigment bettwen indexes) i.e. if x and y have the same prime factors, then