Hello CF community,
I've created the following problem but don't know how to solve it. Though trying for many hours I couldn't figure out how to distribute the component of force when two frictionless planes fall one on another.
Moreover, I've set the constraints low for brute force solutions. But Is there any way to solve it efficiently?
Sorry for my poor English. I hope you find the problem interesting :)
Statement
On this EID li'l Iman has got a box of dominoes from his elder sister. But he doesn't know how to play dominoes. As he has a lot of enthusiasm for physics so he started to do an experiment with it.
He put all dominoes side by side on a rigid plane numbered from left to right. Then he slowly lifts the left end of the plane. At some point a domino will fall and touch the next domino(if there is any) then a chain reaction starts and all dominoes will fall.
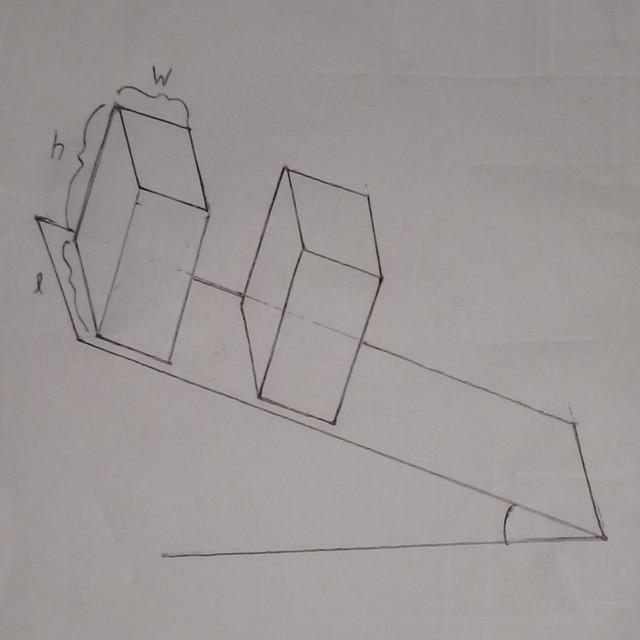
There will be n dominos in a box. Hight, length, and width of each domino are h, l, w. Density of ith domino is di. All dominos are evenly dense.
Now li'l Iman wants to know what is the minimum inclined angle at which kth domino will fully touch the ground and what would be its speed when it will fully be on the ground. As Iman is not good at calculation he asks you to solve this problem.
In this experiment, the plane and the surface of the domino will have friction and the surface between two dominoes and between domino and ground will not have friction. Moreover, It is guaranteed that the static friction between the plane and domino is high enough not to slip back. The gravitational acceleration is g = 9.8 ms-2 and coefficient of static friction between domino and plane is 0.43.
Input
The first line contains n, k (1 <= n, k <= 102), denoting the number of dominoes and the domion at which Iman is interested in. Next line contains 3 integers: h, l, w (1 <= w <= l <= h <= 1000) followed by a new line containing n positive integers di <= 1000, density of ith domino. The distance between two dominoes is (h — w).
Output
Print two real numbers, the minimum inclined angle and the speed of kth domino on the ground, on a single line separated by a single space.










