I am happy to present you author's ideas of solutions. Editorial of the first five problem is authored by — HolkinPV and gridnevvvit, editorial for the last two problems is written by me.
479A - Expression
In this task you have to consider several cases and choose the best one:
int ans = a + b + c;
ans = max(ans, (a + b) * c);
ans = max(ans, a * (b + c));
ans = max(ans, a * b * c);
cout << ans << endl;
479B - Towers
The task is solved greedily. In each iteration, move the cube from the tallest tower to the shortest one. To do this, each time find the position of minimum and maximum in the array of heights (in linear time).
479C - Exams, 480A - Exams
The solution is again greedy. Sort the exams by increasing ai, breaking ties by increasing bi. Let’s consider exams in this order and try to take the exams as early as possible. Take the first exams in this order on the early day (b1). Move to the second exam. If we can take it on the day b2 (i.e. b1 ≤ b2), do it. Otherwise, take the second exam on the day a2. Continue the process, keeping the day of the latest exam.
std::sort(a, a + n); // а is the array of pairs, where first element is the date in schedule, and second is the early date of passing
int best = -1;
for(int i = 0; i < n; i++) {
if (best <= a[i].second) {
best = a[i].second;
} else {
best = a[i].first;
}
}
479D - Long Jumps, 480B - Long Jumps
It is easy to see that the answer is always 0, 1 or 2. If we can already measure both x and y, output 0. Then try to measure both x and y by adding one more mark. If it was not successful, print two marks: one at x, other at y.
So, how to check if the answer is 1? Consider all existing marks. Let some mark be at r. Try to add the new mark in each of the following positions: r - x, r + x, r - y, r + y. If it become possible to measure both x and y, you have found the answer. It is easy to check this: if, for example, we are trying to add the mark at r + x, we just check if there is a mark at r + x + y or r + x - y (by a binary search, since the marks are sorted). Make sure that the adde marks are in [0, L].
479E - Riding in a Lift, 480C - Riding in a Lift
The task is solved by a dynamic programming. State is a pair (i, j), where i is the number of trips made, and j is the current floor. Initial state is (0, a), final states are (k, v), where v is any floor (except b).
It is easy to see the transitions: to calculate dp(i, j), let’s see what can be the previous floor. It turns out that all possible previous floors form a contiguous segment (with a hole at position j, because we can’t visit the same floor twice in a row). So, dp(i, j) is almost equal to the sum of values dp(i - 1, t), where t belongs to some segment [l, r] (the values of l and r can be easily derived from the conditions from the problem statement). Using pretty standard technique called “partial sums” we can compute dp(i, j) in O(1), so overall complexity is O(NK).
Jury solution: 8322623
480D - Parcels
Let’s make two observations.
First, consider the parcels as time segments [ini, outi]. It is true that if at some moment of time both parcel i and parcel j are on the platform, and i is higher than j, then  .
.
Second, let’s imagine that there are some parcels on the platform. It turns out that it is enough to know just a single number to be able to decide whether we can put another parcel on top of them. Let’s denote this value as “residual strength”. For a parcel (or a platform itself) the residual strength is it’s strength minus the total weight of parcels on top of it. For a set of parcels, the residual strength is the minimum of individual residual strengths. So, we can put another parcel on top if it’s weight does not exceed the residual strength.
These observations lead us to a dynamic programming solution. Let the top parcel at the given moment has number i, and the residual strength is rs. Make this pair (i, rs) the state of DP, because it is exactly the original problem, where the platform strength is rs and there are only parcels j with  . In d(i, rs) we will store the answer to this instance of the original problem.
. In d(i, rs) we will store the answer to this instance of the original problem.
Which transitions are there? We can choose a set of parcels i(1), i(2), ... i(k) such that
- outi(j) ≤ ini(j + 1), i.e. segments do not intersect (but can touch) and are sorted;
- the weight of each of these parcels does not exceed rs.
This choice corresponds to the following sequence of actions: first put parcel i(1) on the top of i. This gets us to the state i(1), min(rs - wi(1), si(1)), so we add up the answer for this state and the cost of i(1). Then we take away all parcels, including i(1), and put the parcel i(2) on top of i, and so on.
As the number of states in DP is O(NS), all transitions should take linear time. It can be achieved by making an inner helper DP. This give a solution in O(N2S). Note that for simplicity the platform can be considered as a parcel too.
480E - Parking Lot
Let’s denote the car arrivals as events.
Consider the following solution (it will help to understand the author’s idea): let’s consider all empty square in the table. There a too many of them, but imagine that we can afford to loop through all of them. If we fix a square, we can find out when it is no longer empty: find the first event that belongs to this square. Let this event has number x, and the size of the square is k. Now we can update the answers for all events with numbers less than x with a value of k.
The model solution use the idea of Divide and Conquer. Let’s make a recursive routine that takes a rectangular sub-table, bounded with r1, r2, c1, c2 (r1 ≤ r2, c1 ≤ c2), and a list of events that happen inside this sub-table. The purpose of the routine is to consider how maximal empty squares in this sub-table change in time, and to update the answers for some of the events.
Let’s assume that c2 - c1 ≤ r2 - r1 (the opposite case is symmetric). Take the middle row r = (r1 + r2) / 2. Virtually split all the squares inside the sub-table into those which lie above r, those which lie below r, and those which intersect r. For the first two parts, make two recursive calls, splitting the list of events as well. Now focus on the squares that intersect the row r.
Using initial table, for each cell (r, c) we can precompute the distance to the nearest taken cell in all four directions (or the distance to the border, if there is no such cell): up(r, c), down(r, c), left(r, c) и right(r, c). Using this values, build two histograms for the row r: the first is an array of values up(r, c), where c1 ≤ c ≤ c2; the second is an array of values down(r, c), where c1 ≤ c ≤ c2. I say histograms here, because these arrays actually can be viewed as heights of empty columns, pointing from the row r upwards and downwards. Lets call the first histogram “upper”, the second one — “lower”. Now consider all events inside the sub-table in the order they happen. Each event changes a single value in a histogram. If after some event x the maximum empty square found in the histograms has size k, and the next event has number y, we can update answers for all events with numbers x, x + 1, ..., y - 1 with the value of k.
It remains to learn to find a maximum square in two histograms. It can be done by a two-pointer approach. Set both pointers to the beginning. Move the second pointer until there is such square in histograms: there is a square with side length k if (minimum on the interval in the upper histogram) + (minimum on the interval in the upper histogram) — 1 >= k. When the second pointer can not be moved any more, update the answer and move the first pointer. To find the minimum in O(1), author’s solution creates a queue with minimum in O(1) support. That is, the maximum square can be found in linear time.
Let’s try to estimate the running time. Each call of the routine (omitting inner calls) costs O(len·q), where len is the shortest side of the sub-table, and q is the number of events in it. If we draw a recursion tree, we will see that each second call len decreases twice. The total cost of all operations in a single level of a recursion tree is O(NK), where K is the total number of events. As long as we have O(logN), overall complexity is O(NKlogN).









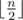 times, than all children can get mittens of distinct colors. One way to construct such solution is to sort all left mittens in the order of decreasing frequency of their colors: for the input 1 2 1 2 3 1 3 3 1 we get 1 1 1 1 3 3 3 2 2. To obtain the sequence of right mittens, rotate the sequence of left mittens to the left by the maximum color frequency (in the example it is 4, so we get the sequence 3 3 3 2 2 1 1 1 1). Then just match the sequences (1 — 3, 1 — 3, 1 — 3, 1 — 2, 3 — 2, 3 — 1, 3 — 1, 2 — 1, 2 — 1). It can be easily shown that all pairs consist of distinct colors.
times, than all children can get mittens of distinct colors. One way to construct such solution is to sort all left mittens in the order of decreasing frequency of their colors: for the input 1 2 1 2 3 1 3 3 1 we get 1 1 1 1 3 3 3 2 2. To obtain the sequence of right mittens, rotate the sequence of left mittens to the left by the maximum color frequency (in the example it is 4, so we get the sequence 3 3 3 2 2 1 1 1 1). Then just match the sequences (1 — 3, 1 — 3, 1 — 3, 1 — 2, 3 — 2, 3 — 1, 3 — 1, 2 — 1, 2 — 1). It can be easily shown that all pairs consist of distinct colors.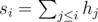 . Then the sum of heights of the planks
. Then the sum of heights of the planks 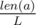 . Let's fix the position
. Let's fix the position 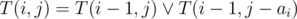 . The
. The 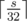 . To get the
. To get the 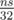 operations. To find the actual way to obtain
operations. To find the actual way to obtain 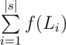 , where
, where 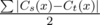 . Now we need to obtain lexicographically minimum solution. Lets iterate through the positions in
. Now we need to obtain lexicographically minimum solution. Lets iterate through the positions in 
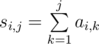 . All these sums can be easily computed in
. All these sums can be easily computed in 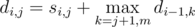 .
. 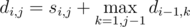 .
. 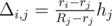 .
.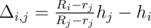 .
.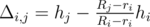 .
.
