Greetings Codeforces Community! We invite you to experience the monthly CodeChef Lunchtime for December. The 3-hour contest will offer 5 challenging problems to solve. It will be a great way to close this year on a happy note with your increased ratings!
The problem statements of the contest will be available in English, Hindi, Bengali, Russian, Mandarin, and Vietnamese. Also, if you have some original and engaging problem ideas, and you’re interested in them being used in the CodeChef's contests, you can share them here: www.codechef.com/problemsetting/new-ideas.
I hope you will participate with your fellow programmers and enjoy the contest problems. Joining me on the problem setting panel are:
Setters: Nguyen Ngoc Trung (chemthan), Rami Alssadaqa (i_love_islam), Hasan Jaddouh (kingofnumbers)
Tester: Roman Bilyi (RomaWhite)
Statement Verifier: Jakub Safin (Xellos)
Mandarin Translator: Gedi Zheng (gediiiiiii)
Vietnamese Translator: Team VNOI (Songuku95)
Russian Translator: Fedor Korobeinikov (Mediocrity)
Bengali Translator: Mohammad Solaiman (solaimanope)
Hindi Translator: Akash Srivastava (devils_code)
Contest Details:
- Start Date & Time: 28th December 2019 (1730 hrs) to 28th December 2019 (2230 hrs). (Indian Standard Time — +5:30 GMT) — Check your timezone.
- Contest link: www.codechef.com/LTIME79
- Registration: You just need to have a CodeChef handle to participate. For all those who are interested and do not have a CodeChef handle, are requested to register in order to participate.
- Prizes: Top 10 Indian and top 10 Global school students from ranklist will receive certificates and CodeChef laddus, with which the winners can claim cool CodeChef goodies. Know more here.
Good Luck!
Hope to see you participating!!
Happy Programming!!









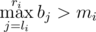 — it's impossible due to construction of array
— it's impossible due to construction of array 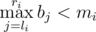 —
— 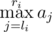 can't be bigger.
can't be bigger.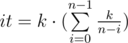
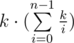
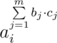 , where
, where 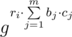 .
.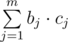 can be equal to all values
can be equal to all values 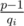 . From the other side it is equal to such minimal number
. From the other side it is equal to such minimal number 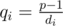 .
.
