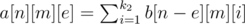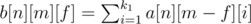Straightforward implementation.
Calculate the answer based on whether the given number is odd or even.
One should observe that inserting a letter at any end of the string is always equivalent to the following operation: we insert an auxiliary (or dummy) letter first, for instance “*”, and then replace it with the desired letter. Besides, in fact we will never need implement any deleting operation, since on one hand, it is not necessary to take a longer string and delete some letters to make it have the same length as our target string; on the other hand, if we have taken the string with the same length, for instance, “abcd”, and the target string is “abce”, instead of first deleting “d” and then inserting “e”, we can directly replace “d” with “e”.
According to the above arguments, we can always only use replacement operations to obtain the target string, with the minimum number of modification. Therefore, suppose that the length of the target string is ul and the given string has length sl. Then, we insert ul auxiliary letters, for instance “*”, both to the head and end of string s to obtain a new string s' with length of 2ul + sl. Next, we check all the substrings of s' with length ul and find the one that has the minimum number of different letters corresponding to the same indices. This number just indicates how many replacement operations should be implemented.
We should first find out all the potential criminals. We check for each person that if he is the unique criminal, whether there are exactly m true claims. By some simple precalculation, we can find all the potential criminals with complexity O(n).
Then, for each person, we check the result of its claim. For “+i”, there are three possible cases: 1) i is the unique criminal; 2) i is not included in the set of potential criminals; 3) i is not the only potential criminal. Similarly, there are also three cases for “-i”, and omitted here.
We can adopt “set” to store the potential criminals, and thus we can handle any of the above cases with complexity of order O(logn).
One can check that no matter how many operations have been implemented, the sum of the string will always be the same. Two strings are equivalent if and only if they have both the same length and the same sum (I did not figure out how to prove this...).
Therefore, we can adopt dfs with memorization. We use dp[i][j] to store the number of equivalent strings that have length i and sum j, while using function dfs(i, j) to denote the number of equivalent strings whose first i letters have sum equal to j. When we reach dfs(i, j), we should recursively call function dfs(i - 1, j - 0), dfs(i - 1, j - 1),..., dfs(i - 1, j - 25), where 0 means letter “a”, and in fact we are enumerating from “a” to “z” for the i-th position (remember to memorize the answers in dp[i][j]).
One could also calculate dp[i][j] in previous, and this is less time comsuming than the above method.
This turns out to be another classic problem !! One can check Caylay's formula for some preliminaries.
This problem can be viewed as an advanced version of Caylay's formula. For the original version, all the nodes are simple nodes, while in this problem, one node may be a “big node”, which in fact is a connected component.
The proof for this advanced version can be found in the Russian tutorials (I use google translation and I think it works quite well)...








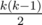 to the final answer.
to the final answer.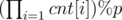 .
.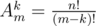 ). Thus, we have
). Thus, we have 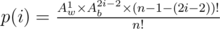 . In general, it is better to transfer the formula to logarithm domain, i.e., we compute
. In general, it is better to transfer the formula to logarithm domain, i.e., we compute 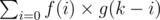 ways.
ways. 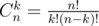 . There is a standard algorithm to compute formula like
. There is a standard algorithm to compute formula like 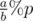 . By using Fermat's theorem, we can transfer it into
. By using Fermat's theorem, we can transfer it into 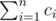 and the total number of adding operations is
and the total number of adding operations is 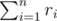 , which gives
, which gives 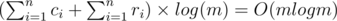 .
.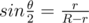 . Thus, we can have
. Thus, we can have 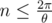 small circles, which is
small circles, which is 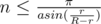 . To avoid wrong answer caused by precision, we can implement
. To avoid wrong answer caused by precision, we can implement 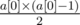 choice. Thus, the final answer should be
choice. Thus, the final answer should be 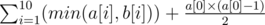 .
.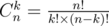 . Although
. Although 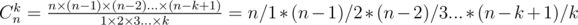 , which could handle all
, which could handle all 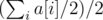 .
.