We keep dividing l by k until l is not a multiple of k any more, and then check whether l is reduced to 1 or not.
As n is limited up to 16, we can use bitmask to enumerate all the feasible combinations and check whether they can form a group or not. The total complexity is O(2n × n2).
This is a straightforward implementation problem. For each given string, we need to check the following conditions.
1) all the words end with the required suffix
2) all the words have the same gender
3) all the words appear in the required order
4) there is exactly one noun word
The idea is to previously calculate all the positions of the required prefix and suffix. Then, we enumerate every pair of feasible combination, and find out all the different substrings.
Therefore, the main task is how to determine whether two strings are the same or not. I did not come up with a good solution, however I studied the other accepted codes.
I found that they adopt an “unsigned long long int” variable x, initialized with zero value, and compute x = x × prime + s[i], where prime is a prime integer. I think this means to transform or map the string to an integer, like hash table. However, I did not figure out how could this guarantee that no two strings are mapped to the same integer, since we have at most 262000 different strings but only 264 integers. Although for some substring of length m, we can in fact only have O(n) different ones, which is quite small compared with 264, but this still can not guarantee that no collisions occur...
There is a standard solution, referred to as “sieve function”, to this problem. Using “bitset” can also solve the memory problem. Instead of testing each prime integer, we can enumerate a and b, and then test whether the result of a2 + b2 is prime or not. The complexity is O(ab) = O(n). To further decrease the constant of complexity, for each value of a, we can start enumerating the value of b from a + 1, with increment step of 2. The reason is that if both a and b are even or odd, the value of a2 + b2 must be an even integer, and thus is definitely not a prime integer.








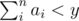 can satisfy the requirement, then
can satisfy the requirement, then 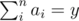 can satisfy as well. Thus, we set
can satisfy as well. Thus, we set  . Moreover, if
. Moreover, if  to obtain all its divisors. For each divisor, we should check whether it is divisible by any one of the previous
to obtain all its divisors. For each divisor, we should check whether it is divisible by any one of the previous 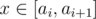 and
and 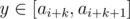 . Therefore, it suffices to count the number of pairs
. Therefore, it suffices to count the number of pairs 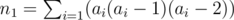 , where all
, where all 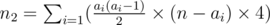 , where
, where 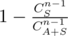 . To compute
. To compute 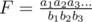 , I usually transform it into
, I usually transform it into 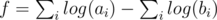 , and then obtain
, and then obtain 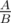 , where both
, where both 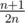 . When there are two bullets, the second one should be put at a position with even index so that the winning probability is not decreased. For more bullets, the strategy is similar as the case where
. When there are two bullets, the second one should be put at a position with even index so that the winning probability is not decreased. For more bullets, the strategy is similar as the case where 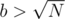 , the complexity is reduced to
, the complexity is reduced to 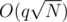 . On the other hand, if all the queries have
. On the other hand, if all the queries have 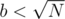 , we can previously use DP algorithm to compute the results for all the potential values of
, we can previously use DP algorithm to compute the results for all the potential values of  .
.  , we use DP algorithm with complexity
, we use DP algorithm with complexity 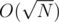 times, which gives complexity
times, which gives complexity 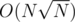 while the latter one might be implemented for at most
while the latter one might be implemented for at most 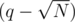 times, which gives complexity
times, which gives complexity 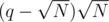 . Therefore, the total complexity has been reduced to
. Therefore, the total complexity has been reduced to 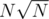 .
.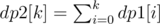 . For a route from node
. For a route from node 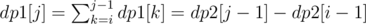 . Therefore, to compute any
. Therefore, to compute any 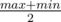 , the current configuration can be recovered.
, the current configuration can be recovered.
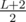 ; otherwise, it implies that we can always find a required integer with the same length
; otherwise, it implies that we can always find a required integer with the same length 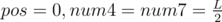 .
. 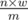 , and also put them in the same manner as mentioned above.
, and also put them in the same manner as mentioned above.  holds, and thus
holds, and thus 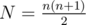 elements. Thus, we should first compute the remainder
elements. Thus, we should first compute the remainder 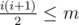 . The answer is
. The answer is  .
. moves. For each minute, at most
moves. For each minute, at most 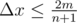 . Given
. Given 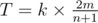 moves. However, the value
moves. However, the value 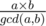 , the two trains meet each other again, and thus it is sufficient to focus only on this time interval.
, the two trains meet each other again, and thus it is sufficient to focus only on this time interval. 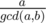 such intervals. Next, we store and update the starting time of train-a in each interval of length
such intervals. Next, we store and update the starting time of train-a in each interval of length  . Thus, we can adopt two pointers to find out all the target intervals, and calculate the answer.
. Thus, we can adopt two pointers to find out all the target intervals, and calculate the answer.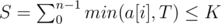 . Moreover, we compute
. Moreover, we compute  . This is the first time that I realized what an important role that a constant can play.
. This is the first time that I realized what an important role that a constant can play.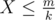 . If we set
. If we set  . Then, we derive the formula as follows:
. Then, we derive the formula as follows: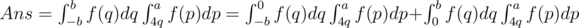
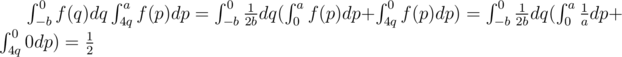 .
.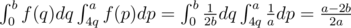
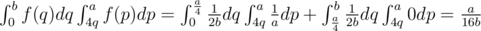
 ;
;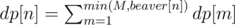 . Moreover, note that we might still have beavers left at both node
. Moreover, note that we might still have beavers left at both node 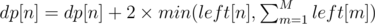 .
. 
