Hello everyone!
I would like to invite you to the competition of Authorship Identification of SOurce COde (AI-SOCO) that is prepared by justHusam, alfadel and myself.

This is no competitive programming competition, but it is very much related to it. :)
This is more of an Artificial Intelligence / Machine Learning competition but it is centered around the Codeforces competitions community and the problems we face.
In this competition, participants are required to build a system that can identify the author of a given source code.
This can help in identifying whether a submitted code in some contest does actually belog to the user who submitted it or not, thus minimizing cheating in Codeforces. =D
The dataset is composed of source codes collected from the open submissions in the Codeforces, we selected 1,000 users and collected 100 source codes from each one. So, the total number of source codes is 100,000. All collected source codes are correct, bug-free, compile-ready and written using the C++ programming language using different versions. For each user, all collected source codes are from unique problems.
For more details on the competition, please visit the website here.
The competition will be organized as a PAN track at FIRE 2020 10 — 13 December Virtual Conference
Best of luck for all participants!









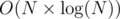 .
.
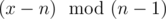 , the remainder cookies. Depending on whether
, the remainder cookies. Depending on whether 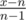 is even or not, I can figure out the direction of the last iteration, and where I start giving (either start
is even or not, I can figure out the direction of the last iteration, and where I start giving (either start 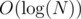 .
.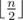
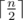 and so on..
and so on.. 
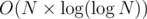 .
. , So we are only interested in
, So we are only interested in 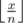 , now we have
, now we have  as left-over which is less than
as left-over which is less than 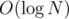 .
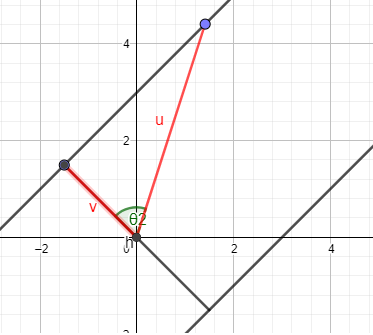
.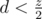 the soldier will intersect with the base, otherwise he will intersect with the left border (imaging a circle at
the soldier will intersect with the base, otherwise he will intersect with the left border (imaging a circle at  ).
). 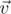 be vector that resembles the left side of the base and
be vector that resembles the left side of the base and 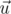 be a vector from
be a vector from 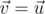 (in terms of direction), else we can get
(in terms of direction), else we can get 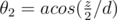 .
. 
 after normalizing
after normalizing  .
. and Left with probability
and Left with probability 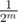 as we have
as we have 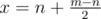 . Now the probability will be
. Now the probability will be  where
where 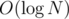 per test case for the multiplicative inverse.
per test case for the multiplicative inverse.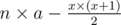 which will be distributed on
which will be distributed on 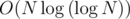 for pre-calculating totient and
for pre-calculating totient and  per query.
per query.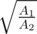 , from which we can find
, from which we can find 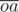 and
and 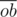 then
then 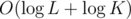 per test case since
per test case since  .
.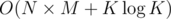 per test case.
per test case. 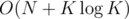 per test case.
per test case. sub-array of only ones, and each of them will add
sub-array of only ones, and each of them will add 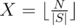 where
where 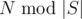 is not zero then we have
is not zero then we have 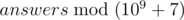 in 2 vectors
in 2 vectors 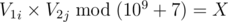 .
.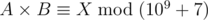 .
. 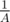 :
: 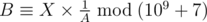 .
. 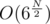 .
. 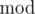 at all, the max hash value will be
at all, the max hash value will be 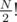 , to eliminate the repeated permutations we divide by the factorial of half of the frequencies for each letter, basic counting math.
, to eliminate the repeated permutations we divide by the factorial of half of the frequencies for each letter, basic counting math.  .
. 
