I see many new people in CP (like me), taking more time thinking on what problems/tag to practice on,

So I recently made a project that shows which areas are weak for particular User and it will recommend User problems based on the user's current rating and the area/tags he/she is weak.

How it works:

• On the Codeforces official web page, they provide various API which we access to get data in machine-readable JSON format. That data is used for this project.

• It fetches details of the user's past submissions of contests as well as practice problems and using that data it shows the weak tags and fetching user's info, using the User's current rank it recommends the problems.

• This project is made using Django and python, so if someone wants to contribute to improving it, here is the Github link Github.

Some Features of this project:

• Log in with the user's code forces handle.

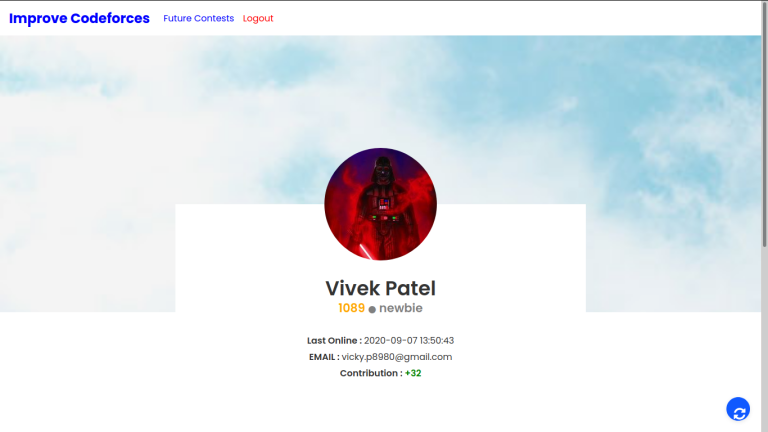
• After submitting the handle, Details of that user and recommended problems are displayed.

• Upon opening, this screen user can perform the following operation -

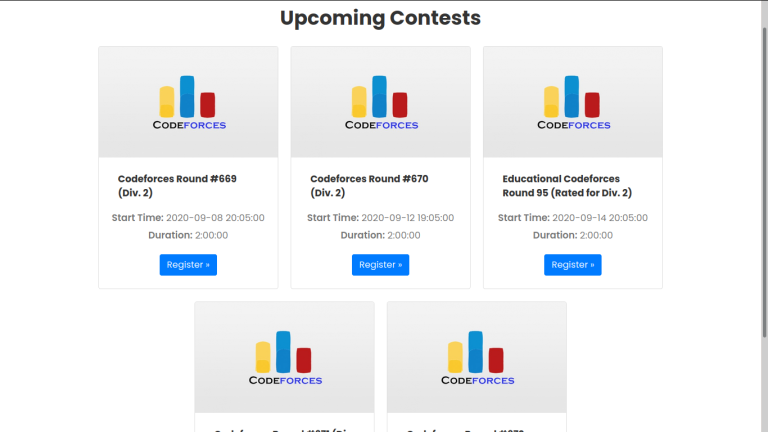
• On clicking on the Future Contest, it will redirect the user to the page where all future contests are listed, and also users can register for the contest.

• User can go to the problems which are recommended and listed on the profile page to solve them.

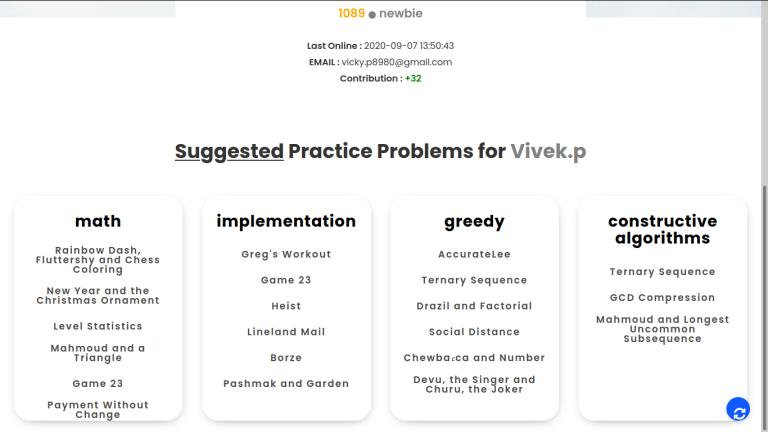
• User can refresh the recommended problems

• Logout

How to install and execute the project on your system, is given in the GitHub readme.md.

So, try this project, the aim is to improve the user's performance in a future contest, by practicing effectively. Here is my github repository.

UPD : I have hosted this site in pythonanywhere : link

Recently, i was solving some mathematical problems from the Hackerrank math's section, And i came up with this formula :

$$$\dfrac{1}{x}+\dfrac{1}{y}=\dfrac{1}{n!}$$$

The question was find the number of positive integral solutions for $$$\dfrac{1}{x}+\dfrac{1}{y}=\dfrac{1}{n!}$$$ equation. You can find the problem here.

My solution :

$$$\dfrac{1}{x}+\dfrac{1}{y}=\dfrac{1}{n!}$$$ , Consider N = n!.

Now,the equation,

$$$\dfrac{1}{x}+\dfrac{1}{y}=\dfrac{1}{N}$$$

∴ $$$\dfrac{x+y}{xy} = \dfrac{1}{N}$$$

∴ $$$N( {x + y} ) = xy$$$

∴ $$${xy - N({x+y})} = 0$$$

Now adding both sides with N^2 :

$$${xy - N( {x + y}) + N^2} = N^2$$$

∴ $$${xy - Nx - Ny + N^2} = N^2$$$

∴ $$${x({y - N}) - N ({y - N })} = N^2$$$

∴ $$$({x - N}) ({y - N}) = N^2$$$

From this equation we know that number solution will be the number of divisiors of N.

That means we only need to find number of divisors of $$$n!^2$$$.

1. Now one way is find value of $$$n!^2$$$ and find the number of divisors of them.But for less time complexity we can find number of divisiors $$$n!^2$$$ by Legendre's formula.

2. For that,

   • Find all prime numbers less than equals to $$$n$$$.Let say prime numbers less than equals to $$$n$$$ : [p,p1,p2,...]
   • For each prime number p find the largest power of it that divides $$$n!$$$. We use below Legendre's formula for this purpose.

The value of largest power that divides p is $$$⌊n/p⌋ + ⌊n/(p1)⌋ + ⌊n/(p2)⌋ + ...$$$

• Let these largest powers are : [e,e1,e2,...]
• So, for number of divisors of $$$n!$$$ the result is $$${({e + 1}) * ({e1 + 1}) * ({e2 + 1}) ...}$$$ .
• And for $$$n!^2$$$ the result will be : $$${({2*e + 1}) * ({2*e1 + 1}) * ({2*e2 + 1}) ...}$$$.

And that is the answer we are looking for.

For example, lets take $$$n=4$$$, $$$n! = 24$$$ and $$$(n!)^2 = 576$$$.

$$$24 = 2^3 * 3^1$$$

Hence no. of factors $$$= (3+1) * (1+1) = 8$$$, which are : [1,2,3,4,6,8,12,24].

For $$$576 = 2^6 * 3^2$$$,

it is $$$(2*3 + 1) * (2*1 + 1) = 21$$$;

Hence for $$$\dfrac{1}{x}+\dfrac{1}{y}=\dfrac{1}{4!}$$$ this equation total number of positive integral solution are $$$21$$$.

So, that was my answer for the question,Correct me if i am wrong.

Here is more information about finding divisors of $$$n!$$$.

Many of us believes that solving more problems from problem set will increase our coding ability. So, we start solving as many problems as possible every day. But is it worth doing such hard work?

 Well for me, when I started solving problems on code forces, I also believe that it will increase my rating fast. I decided to do 10 problems every day, and of course to compete with my friends. Many of us do that. But then I see no change in my problem-solving time in contest. I can do “only 2” problems out of 5 in a contest, max “3”.

 So, what goes wrong here?

 When we think to solving more problems a day, we started sorting problems based on difficulties like first 600,700, then 800 and so on.so we only solve the problems which are easier to solve and which we can solve faster. So, in contest we can perform good in only type “A” and “B” problems. There are many problems of difficulties less than 1000 so it will take long time to solve it all and your performance will not increase.

 So I think you should try to solve more problems of Type “B” and “C” if you are a beginner, because we can easily solve “A” questions, it will help you more rather than solving as much problems as possible. Practice lots of problems which are harder for you to solve and continue to feel challenged. It will surely increase your competitive coding strength.

 So solving more problems will not improve you , solving better problems will.

I found this Quora article very helpful if you need more information : Link

I saw many people using this line before their code! ios_base :: sync_with_stdio(false), cin.tie(NULL), cout.tie(0) I think it is for fast input /output.But how it works?