Today at 11:00 AM EST takes place SRM #608.
By the coincidence it overlaps with the opening ceremony of Winter Olympic Games in Sochi.
| # | User | Rating |
|---|---|---|
| 1 | ecnerwala | 3649 |
| 2 | Benq | 3581 |
| 3 | orzdevinwang | 3570 |
| 4 | Geothermal | 3569 |
| 4 | cnnfls_csy | 3569 |
| 6 | tourist | 3565 |
| 7 | maroonrk | 3531 |
| 8 | Radewoosh | 3521 |
| 9 | Um_nik | 3482 |
| 10 | jiangly | 3468 |
| # | User | Contrib. |
|---|---|---|
| 1 | maomao90 | 174 |
| 2 | awoo | 164 |
| 3 | adamant | 162 |
| 4 | TheScrasse | 159 |
| 5 | nor | 158 |
| 6 | maroonrk | 156 |
| 7 | -is-this-fft- | 151 |
| 8 | SecondThread | 147 |
| 9 | orz | 146 |
| 10 | pajenegod | 145 |
Today at 11:00 AM EST takes place SRM #608.
By the coincidence it overlaps with the opening ceremony of Winter Olympic Games in Sochi.
Round starts in 10 minutes.
Seems like everybody related to the event already knows, but anyway I'll remind.
Facebook Hacker Cup Round 3 is happening today at 1:00 PM PT. Top-25 coolhackers will continue to Final Round.
Today at 11:00 AM EDT will be TopCoder Test SRM.
What does Test SRM mean? It is still rated, isn't it?
Today is going to be SRM #577 (at 03:00 UTC).
Let's discuss problems in this topic when round ends.
Hello!
Does anyone have test data for BOI 2012? Links on official site are broken :-(
Also I didn't find any contacts there. Maybe somebody has e-mail, or any contact of jury of that olympiad?
UPD: there can be some type of misunderstanding. I mean Baltic Olympiad in Informatics, not Balkan.
Hi everyone! I wan't to share some interesting fact about how we're going to challenge almost every solution, that uses polynomial hashes modulo 2^64. We'll hack any solution, regardless of it's base (!), the only thing we need, that it's using int64 with overflows — like many coders write hashing.
Keywords: Only today, only for you, ladies and gentlemen: we're gonna challenge Petr's solution in problem 7D - Palindrome Degree from Codeforces Beta Round #7!
Is it interesting? Welcome reading after the cut.
Tomorrow in Hungary starts CEOI 2012 — Central-European Olympiad in Informatics. It's very interesting contest, problems are quite hard in comparsion to other school olympiads. There will be internet-contest on same problemset: first tour at 9th July, second at 11th July; both tours will start at 08:00 UTC.
Rules — like on old IOI with test groups (group scores only if all tests in that group passed)
Registration closed tomorrow (08 July) at 18:00 UTC!
UPD: (possibly) rules changed this year.
UPD2: you should have recieved e-mail wih password and instructions. Rules indeed were updated.
UPD3: Contest server is veeeery slow so here is the mirror for the tasks (thx to popoffka):
UPD4: Here is mirror for second day statements (thx to yeputons):
Hello everybody. Here's my simple userscript, that highlights viewed submits in tables.

PavelKunyavskiy suggested to make it public.
Because it's not good to send additional AJAX queries to the server, functionality is quite little. Submit becomes marked after opening it's table cell. Unique-hash of submit is (user, problem, time), so submits, made in same minute, seems identical. I don't think it's a big problem :-)
Everybody who doesn't like default style can adjust it in function color.
It works in Firefox in Greasemonkey, in Chrome by default. Don't know about Opera, though.
I can improve something. Use it :-)
UPD1: Now by ctrl-click as good as by double-click
UPD2: Now works under Opera.
Summer finally has come! So I want to tell about cool summer Internet Problem Solving Contest or IPSC. It's very interesting internet-contest. You can participate as a part of the team, or individually; there is also secondary school division on same problemset, but with separate results.
Usual problem are algorithmic output-only, but there are also some tricky challenging. As example, in previous contest there was problem where you had to take care about your dog — right answers decreased your penalty on 20 minutes, incorrect answer would cause death of your animal :-)
Today, June 1 at 08:00 UTC starts practice tour. It's recommended to everyone to participate in it, there are also interesting tricky (previous year) problems.
Contest starts at 10:00 UTC 2 June. GL & HF!
Our teams:
SPbSU4 (Dmitry_Egorov, PavelKunyavskiy, yeputons)
Endeavour to Jump Together (tatyanakov, Goshish, Malinovsky239)
Ide (yarrr, caustique, ant.ermilov)
unusual (eduardische, nvilcins, gen)
Ponyville Coders (ivan.popelyshev, halyavin, iroro)
Red-headed Leage (tunyash, Skird, fdoer), homo_sapiens(Edvard)
Individual: Scorpy (Scorpy), Gerald (Gerald), homo_sapiens(Edvard)
GCJ Round 2 starts today at 14:00 UTC. It's a good chance to take cool T-Shirt, just place 1000 or higher. Top 500 contestants will advance to Round 3.
Yesterday at 14:00 GMT starts first internet-round of COCI - Croatian Open Competition in Informatics. As usual, it will contain 6 problems for 3 hours. Testing system - like in old IOI (without feedback, each test is rated separately).
There isn't nothing really hard in registering - just registering in testing system and logging in COCI Contest #1.
From myself: I like that contests. Great, tasty problems with right rating system :-)
Thanks to yeputons for undistinguished idea of publishing about COCI on CF.
For those who don't know yet. Yesterday morning Steve Jobs died.
It's hard to estimate what he done for IT for his life. It's very sad that so great people die.
Sometimes I think about such a question. We are solving one-thread contests: we solve all problems without parallel programming.
But is there any contest with problems for parallel algorithms? I think it would be quite interesting. Does anybody know?
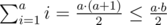 . Besides, the equality is fulfilled when the following condition is met: b - a = 1.
. Besides, the equality is fulfilled when the following condition is met: b - a = 1. 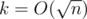 simple linear equations for each number of piles after splitting. We can construct all the divisions in advance, simply taking one by one the smallest pile and the number or piles and terminating when the sum exceeds n. The second way is better because it works for the O(m + n), where m stands for the number of edges, and the first one works for
simple linear equations for each number of piles after splitting. We can construct all the divisions in advance, simply taking one by one the smallest pile and the number or piles and terminating when the sum exceeds n. The second way is better because it works for the O(m + n), where m stands for the number of edges, and the first one works for 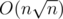 , which is larger.
, which is larger.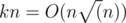 . However, in practice they are much less - about 520 thousand. Which is why there's enough time to build the edges within the time limit of O(nk).
. However, in practice they are much less - about 520 thousand. Which is why there's enough time to build the edges within the time limit of O(nk).Problem Div1-E. Mogohu Ree Idol.
In this task we had to verify that the point is the centroid of the triangle formed by points of the given three polygons. Lets reformulate the problem. We should verify the existence of three points A, B, C, such that A belongs to the first polygon, B - to the second one, C - to the third one, and 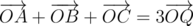 . Logically, you should understand what set of points determines this
. Logically, you should understand what set of points determines this 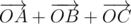 , you should understand how to build it and test a point on whether it belongs to the set or not. This set is called Minkowski sum. We will need only one of its properties: the sum of two convex polygons is a convex polygon whose sides coincide as vectors, with the sides of the original polygons. We will prove this later.
, you should understand how to build it and test a point on whether it belongs to the set or not. This set is called Minkowski sum. We will need only one of its properties: the sum of two convex polygons is a convex polygon whose sides coincide as vectors, with the sides of the original polygons. We will prove this later.
How do we use it now? The first thing that this property gives us is an algorithm to test for belonging. Once the sum is built you can test whether or not a point belongs to the sum using a standard algorithm of testing a point being inside of a convex polygon in logarithmic time. Also the constructing algorithm is immediately obtained. We just need to add the coordinates of the lowest (the leftmost of them) points of all three polygons. As a result, we get a point, which is the lower left for the sum polygon. The sides are now represented as a sorted by the polar angles list of parties of the original polygons (instead of sorting we may merge sorted arrays).
Proof.
We shall prove the correctness of the algorithm for two polygons, for three polygons the proof is just the same. Let the first polygon be represented by A and the second one - by B. Denote the sum as M.
We will prove that M is a convex set.
Choose some 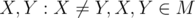 . By definition,
. By definition, 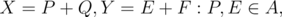 Q,
Q, 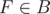 (here and below the point is identified with its radius vector).
(here and below the point is identified with its radius vector).
Let’s take some point 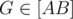 . We shall prove that
. We shall prove that 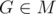 .
.
As G lies on the [AB], 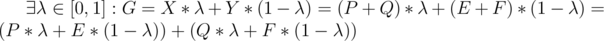 .
.
Note that the first bracket is obviously some point lying on the segment [PE]. That means the point lying inside the polygon A, since A is convex. Similarly, the second bracket is inside B. Hence, their sum, i.e., G, lies in the Minkowski sum. This means that the Minkowski sum is a convex set.
Let us consider some side XY of the first polygon. Let's rotate the plane so that the side XY was horizontal and that the polygon lied above the XY line.
Consider the lowest horizontal line intersecting B. Let it cross B along the segment of PR, where point P does not lie further to the right of the R (it is clear that PR can turn out to be a degenerate segment from one vertex or the segment between two consquent verteces). Let's call PR the lowest segment of the polygon. Then we construct in the similar way the lowest segment UV of polygon M.
Let's prove that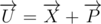 - if not, let
- if not, let 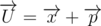 . It is clear that x and p are the lowest points of the polygons A and B - otherwise one of them can be moved to a small vector d, which lies in the lower half-plane, so that the point remained within its polygon. In this case U will move the same way to d, which contradicts the fact that U is one of the lowest points of the polygon.
. It is clear that x and p are the lowest points of the polygons A and B - otherwise one of them can be moved to a small vector d, which lies in the lower half-plane, so that the point remained within its polygon. In this case U will move the same way to d, which contradicts the fact that U is one of the lowest points of the polygon.
Thus, x and p are the lowest points of their polygons. Similarly, x and p are the leftmost points on the lowest segments of their polygons - otherwise we shift x or p to vector d that is directed to the left. It is also a contradiction - the U point stops to be the leftmost lower point.
Hence, U = X + P. Similarly, V = Y + Q. Hence, 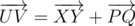 .
.
Thus, the sequence of sides M as vectors in the, for instance, counterclockwise order, is nothing other than the union of sides of A and B as vectors in the counterclockwise order, that immediately proves the correctness of the algorithm.
| Name |
|---|


