Seems like everybody related to the event already knows, but anyway I'll remind.
Facebook Hacker Cup Round 3 is happening today at 1:00 PM PT. Top-25 coolhackers will continue to Final Round.
| # | User | Rating |
|---|---|---|
| 1 | ecnerwala | 3649 |
| 2 | Benq | 3581 |
| 3 | orzdevinwang | 3570 |
| 4 | Geothermal | 3569 |
| 4 | cnnfls_csy | 3569 |
| 6 | tourist | 3565 |
| 7 | maroonrk | 3531 |
| 8 | Radewoosh | 3521 |
| 9 | Um_nik | 3482 |
| 10 | jiangly | 3468 |
| # | User | Contrib. |
|---|---|---|
| 1 | maomao90 | 174 |
| 2 | awoo | 164 |
| 3 | adamant | 162 |
| 4 | TheScrasse | 159 |
| 5 | nor | 158 |
| 6 | maroonrk | 156 |
| 7 | -is-this-fft- | 151 |
| 8 | SecondThread | 147 |
| 9 | orz | 146 |
| 10 | pajenegod | 145 |
Seems like everybody related to the event already knows, but anyway I'll remind.
Facebook Hacker Cup Round 3 is happening today at 1:00 PM PT. Top-25 coolhackers will continue to Final Round.
| Name |
|---|



Man, that was... definitely harder problems than last year. No AC on the 2nd problem...
I solved the 1st problem with O(K2C) dynamic programming, taking (number of processed families, number of gifts added between them) as a state; C is some large constant here, if we consider the size of a family to be constant — and small.
I realize that if the 2nd problem looks really easy, costs that many points, and is in the last round, it will be something really hardcore, so I never even tried to code anything on it :D
I spent most of the time on the 3rd problem, and managed to prove that the graph must be bipartite, planar (there's no solution for K3, 3) and got to the assumption that is must be reducible to a single edge by the operation "find 2 connected vertices of degree 2 and delete them". Is it good or completely off-topic? :D
Still, top 50 is good enough...
How have you proven that graph must be planar?
I proved that satisfying the main condition for K3, 3 (as a subgraph) leads to a contradiction.
I'll assume you know the trivial rules for vertices at distance 1.
Firstly, a lemma about K2, 2: let's say that one partition of a subgraph K2, 2 contains vertices (1,2) and the other (3,4); w.l.o.g., associate vertex 1 with a subset S1 of chains, such that no other vertex is associated with a smaller set. Then, for vertices 3 and 4, we have S3 = S1 + a and S4 = S1 + b (a, b are also chains, and a ≠ b), and then S2 = S1 + a + b, because if S2 didn't contain (w.l.o.g.) a, then S2 = S1, which is impossible.
I just realized there's a stroger version, working on any subgraph K2, 3. Let's use the same notation as above (partitions (1,2) and (3,4,5)); S3 = S1 + a, S4 = S1 + b, S5 = S1 + c. There are 2 possible cases: |S1| is the smallest or |S3| is the smallest (w.l.o.g.). If it's S1, then by the lemma on K2, 2 (1,2,3,4) and (1,2,3,5), we have S2 = S1 + a + b = S1 + a + c; otherwise, by the lemma on (1,2,3,4) and (1,2,3,5), we have S4 = S3 + a + b = S5; both are contradictions. QED.
My mistake, it doesn't imply planarity. K3, 3 can be a subgraph of a minor, it just can't be a direct subgraph.
Edge contraction affects the solution, so its off-topic.
It's not edge contraction, though. It's edge deletion. I don't merge the endpoints of an edge, I delete them both.
And just to make this clear: leaves are trivial, so I only consider graphs without leaves.
The fact the graph should be planar isn't true. 5-dimensional binary cube (vertices are numbers from 0 to 31, edges between pair of integers if they differ in exactly one bit) isn't planar, but is easily colorable.
Yeah, my mistake. I just confused the rules of planarity a bit. Still, the planarity was just a peculiar note, not anything important :D, what I was proving back then was non-existence of K3, 3.
Could you elaborate on the first problem. I don't see how your state in dynamic programming is sufficient. My understanding is that it's also important how the other gifts (those that were not added between the processed families) are distributed.
Yes, it is important. It's all hidden in the large constant.
Let's say that we're processing family i, and there are j people so far that haven't given/received (those 2 numbers are equal) any gifts. Out of ni people of this family, x can give gifts to processed people, and y can get gifts from the processed people, moving to a state (i, j + ni - x - y).
Now, combinatorics ensues. Let's assume that the conditions of at least 1 way existing (x, y ≤ j, ni etc.) are satisfied. There are ways to choose the x people,
ways to choose the x people, 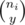 ways to choose y and those 2 groups are independent. There are j(j - 1)..(j - x + 1) ways to choose which people of the j will get gifts from our x, and j(j - 1)..(j - y + 1) ways to choose the same for those giving gifts to the y. Those are just small products and can be enumerated with modular arithmetic in O(ni) = O(1) time.
ways to choose y and those 2 groups are independent. There are j(j - 1)..(j - x + 1) ways to choose which people of the j will get gifts from our x, and j(j - 1)..(j - y + 1) ways to choose the same for those giving gifts to the y. Those are just small products and can be enumerated with modular arithmetic in O(ni) = O(1) time.
So even if there are many ways, those are compressed to the combination-variation product; in the dp state, they're viewed as equivalent and they're differentiated only when picking some few of them.
Funny that C appeared on team competition in Poland 2 weeks ago :P (problem M here http://www.mwpz.poznan.pl/zadania.php). In slightly different version, but main idea was exactly the same. Nobody solved it during the contest, but few guys successfully googled it :P.
Also, Wikipedia had the answer to the problem.
http://en.wikipedia.org/wiki/Partial_cube
Here's a solution to Pizza Baking (the second problem).
Let S_i be the total number of pizzas that need to be in an oven at time i. Then the key lemma to this problem is that the number of ovens needed to satisfy the requirements is always max(ceil(S_i / C_i)). While it's an obvious lower bound I still don't have a clean proof of its correctness.
Given this lemma, we first calculate the number of required ovens, call it M. Then we'll add a virtual pizza at every time so that S_i = C_i * M at all times. Therefore it will be necessary to fill every oven to maximum capacity at all times.
We can find such an assignment that fills the oven to capacity using max flow. To do so we will have K + 1 nodes for each time. Then for each pizza we'll connect its start time to its end time (where the times are in [s, e) form instead of the [s, e] form given in input). Now imagine that there are capacities from the source to the time nodes and from the time nodes to the sink node. Then we can compute the number of pizzas selected by the flow at time i as sum[j<=i] flow[source][j] — flow[j][sink]! Therefore we just need to setup the capacities from the source and sink nodes to time nodes so that in a maximal flow the oven is at capacity at all times.
Therefore we should set cap[source][i] = max(0, C[i] — C[i — 1]) and cap[i][sink] = max(0, C[i — 1] — C[i]).
Now we use this flow concept and try forcing pizzas to be used and verifying that a feasible solution still exists. If we reuse old flow networks this can lead to a rather efficient solution.
Code: https://gist.github.com/msg555/8078816
It was pointed out to me that the max flow construction itself is a proof. We can always saturate the network with fractional flows because S_i is a multiple of C_i and therefore there is an integer solution as well.
Is there any link to the problems too?
T-Shirts are coming! Got mine today.
Anybody knows, it is OK that i have not received my t-shirt yet?
Yeah, sending t-shirts always takes a lot of time for some reason.