We will hold AtCoder Beginner Contest 258.
- Contest URL: https://atcoder.jp/contests/abc258
- Start Time: http://www.timeanddate.com/worldclock/fixedtime.html?iso=20220702T2100&p1=248
- Duration: 100 minutes
- Number of Tasks: 8
- Writer: Kodaman, PCTprobability, physics0523, chokudai, kyopro_friends, m_99, nok0, YoshikaMiyafuji
- Tester: physics0523, Nyaan
- Rated range: ~ 1999
The point values will be 100-200-300-400-500-500-600-600. We are looking forward to your participation!










G is a well-known problem, see https://youtu.be/BJhzd_VG61k?t=3841
You can use bitsets too. It's much more easier to implement.
Well, this solution has complexity $$$O(M*sqrt(M))$$$ where $$$M$$$ can be $$$N^2$$$. Thus, I don't think this solution with $$$O(N^3)$$$ complexity will work.
Just noticed many $$$O(N^3)$$$ solutions passed.
Example
Atcoder Implementation contest :/
LoL dude I took a class Big Data Processing and learned counting triangles this spring semester.
And I solved G today.
G can be solved using bitset
Thanks for the contest, Problem E was great :) even couldn't solve it in the contest due to a small bug in my code but I enjoyed solving it :)
how to solve E ?
You can precompute the number of potatoes in a box if you start with the $$$i$$$'th potato, and then use binary lifting to quickly find which potato the $$$K$$$'th box starts with.
Can you share the link to your code , I want to see how to use binary lifting for this case .
Link
I forgot to put the ll in (1ll<<k). It's so frustrating...... Link
You don't really need binary lifting to figure out the starting point, there will be a few initial starting points, and after that, we will get a cycle so we can simply find out the starting point based on k%cycleSize.
can you please explain a bit more? can't properly grasp what's happening
Notice that there can be atmost N start points across all boxes , so you will get a cycle of length almost N so now , for each N cycles you can find the no. Of gifts(or whatever it was) in that box in LogN time. And during query print the answer corresponding to that box.
Taking the sample test case :
ordering of filling would be : (0 + 1), (2 + 0 + 1), (2 + 0 + 1), (2 + 0 + 1), ...
If we observe that the order filling of potatoes in the boxes would repeat after a period. Here the order of filling started repeating after 2nd box.
so, we would need to find the index from the order, start repeating, and the size of the cycle.
And for answering the query in O(1) we can precompute the order of filling till the cycle.
Here is my solution.
Problem C : https://codeforces.com/problemset/problem/1681/B
What is the observation or logic behind problem F? I even don't know how to start the first step to analyze this problem :(
Is there a solution to G — Triangle without using bitset?
See this https://youtu.be/BJhzd_VG61k?t=3841
See this comment
For problem G — Triangle. I was trying to solve it using bitset.
Can any one explain why Code 1 is giving correct output while code 2 is giving wrong output?
PS:- Found the mistake. In code 2 I need to reverse the string before converting it to bitset.
Anybody can help me with the B problem. I couldn't figure it out till the end.
Since the grid is fairly small we can solve the problem by brute force. Just check each direction starting at each position, which runs foreach direction in $$$O(N^3)$$$
Can somebody tell what is the approach used in E to find the k th box's weight
In E we need to observe that the potato sizes $$$w[]$$$ define a linked list, where each element points to the first potato of the next box. Find the number of each box by binary searh in $$$O(logn)$$$
With this linked list, the problem asks basically for the $$$(K-1)$$$-th successor of the first element. This can be solved by binary lifting
An alternative solution instead of binary lifting can also be construct. We see that starting from first element the linked list leads into a circle at some time. So, there is kind of a tail of size $$$y$$$ leading into a circle of size $$$x$$$.
If $$$K<=y$$$ then answer is the K-th vertex in the tail, else it is the $$$((K-y)\%x)$$$-th vertex of the circle.
Can you please explain why you have used the parent of initial j th element as distance from start but not the size of the box having x weight starting from i?
I think it is the same. The linked list points at each position i to the first potato j of the next box if i was the first potato in the box.
So j=i+size, but also j is the absolute distance from the first potato.
Will the test cases for recent abc's not get added to the dropbox?
How to solve H?
Firstly, lets think about the corner case: $$$N = 0$$$.
We need to split $$$S$$$ into odd terms. Define $$$f(n)$$$ — number of "odd" splits of n.
We can calculate $$$f(n)$$$ using DP (fix first term):
Ok, these are just Fibonacci numbers, we can calculate them using the standard matrice approach in $$$O(\log X)$$$.
Now, we can image this problem as in the picture below:
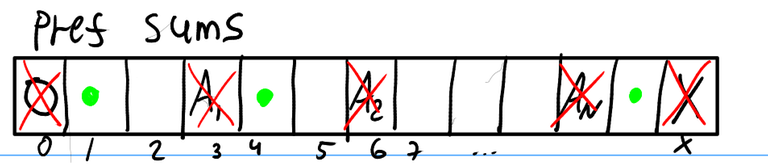
We need to select a few available positions of prefix sums for our array (maybe 0) and make sure that the difference of the neighboring ones (these are exactly the elements of the array) is odd.
Firstly, insert $$$0$$$ and $$$X$$$ into $$$A$$$.
We can calculate $$$dp[i][j]$$$ — number of ways to select free positions $$$0 < p_1 < p_2 < \ldots < p_k < A_i$$$ and
1. $$$p_i - p_{i-1} \equiv 1 \mod 2 $$$
2. $$$A_i - p_k \equiv j \mod 2$$$.
Then, $$$dp[N][1]$$$ is answer.
To recalculate $$$dp[i+1]$$$, in fact, we need to solve this task with $$$N=0$$$. This is quite simple to do using the comments above. It may be necessary to consider several cases, but they are essentially the same.
Sample code
Hey can someone help me out with problem E, I am not able to understand where I am going wrong, this is my Submission, any counter case will also help.
2 1 100
1 1
1
101
100