Hello codeforces!
I am trying to learn the Li Chao tree, but there is a part i am unable to understand. All the resources that i found (e.g: cp-algo) describe it by using two lines. With two lines, it makes sense, because one of them will dominate at most one of the two halves, and in this way, we would have to update only one half (similar to segment trees). Although, that is not always the case when there are more lines. I will describe what i mean with an example (check the image below). Let's say, that the blue lines were inserted before, and now we want to insert the red line. In our case, the red line dominates the green highlighted segment that is on both the left and right part of the total range. In the implementation that the sites provide, we always choose to move to one side and thus maintain logarithmic time. But in the case i describe, we should update both the left and the right part.
What am i missing?
Thanks! 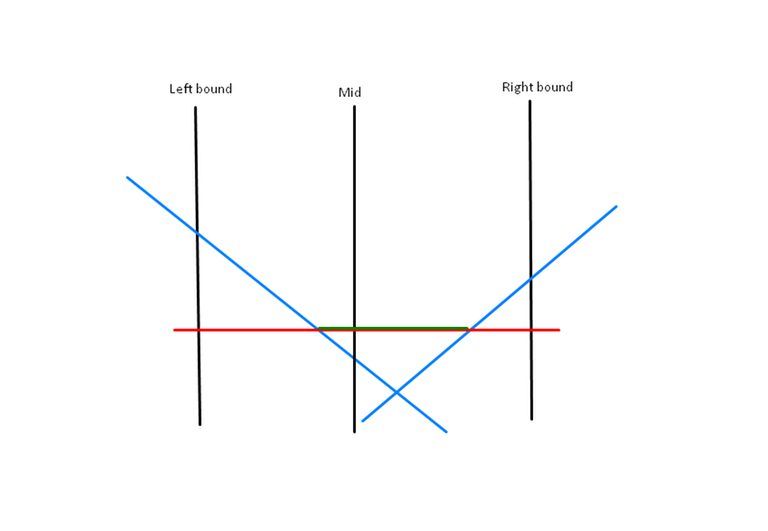
→ Pay attention
→ Top rated
| # | User | Rating |
|---|---|---|
| 1 | ecnerwala | 3649 |
| 2 | Benq | 3581 |
| 3 | orzdevinwang | 3570 |
| 4 | Geothermal | 3569 |
| 4 | cnnfls_csy | 3569 |
| 6 | tourist | 3565 |
| 7 | maroonrk | 3531 |
| 8 | Radewoosh | 3521 |
| 9 | Um_nik | 3482 |
| 10 | jiangly | 3468 |
→ Top contributors
| # | User | Contrib. |
|---|---|---|
| 1 | maomao90 | 174 |
| 2 | awoo | 164 |
| 3 | adamant | 162 |
| 4 | TheScrasse | 159 |
| 5 | nor | 158 |
| 6 | maroonrk | 156 |
| 7 | -is-this-fft- | 151 |
| 8 | SecondThread | 147 |
| 9 | orz | 146 |
| 10 | pajenegod | 145 |
→ Find user
→ Recent actions
↑
↓
Codeforces (c) Copyright 2010-2024 Mike Mirzayanov
The only programming contests Web 2.0 platform
Server time: Apr/24/2024 22:18:40 (i2).
Desktop version, switch to mobile version.
Supported by
User lists


| Name |
|---|











In each segment you store only one line, not many.
Yes, i understand that, but how does this change things? In the example above, wouldn't we still have to go through both children to update them? Previously, for the segments [L,MID] & (MID, R] each of the blue lines was the dominant, but now we would have to go deeper for both children to correctly update for the red line.
the first idea is that in a node you keep a function that cannot be maximal beyond the bounds of l, r
the second idea is that when executing a get request, you get the maximum value of all the functions from all the visited tree nodes on the way to the leaf, and because of this, you have to update only one subtree (in which current function is possible can dominate).
Oh okay, i understand now. The second idea is what i was missing. Indeed, it is clear that taking the maximum out of all the nodes in the path from the root to the leaf would result in the max answer (i totally missed this part). Thank you!