Lets start from the end.
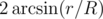 .
.
So, the three stadiums are observed at the same angle if R1 / r1 = R2 / r2 = R3 / r3.
Take two different points A, B. The set of points C that AC / BC = const is either a line (perpendicular bisector of AB) or a circle with center somewhere on the line AB. This circle is easy to find. It contains two points that lie on AB and satisfy AC / BC condition.
Let X1 be the set of points from which stadiums 1 and 2 are observed at the same angle. Let X2 be the set of points from which stadiums 2 and 3 are observed at the same angle. The answer belongs to both X1 and X2 . The centers of the three stadiums don't lie on one line, so the number of points in the intersection of X1 and X2 will be finite.
Check them all. The answer is the point that lies closer to any of the stadiums. The stadiums don't intersect, so that point will not lie inside any of them.
How to get a big circle for X1 : put the centers of the stadiums in the points far away, for example in (0, 0) and (1000, 0). The ratio of the radii should be the closer possible to 1, for example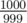 . The center and the radius of the new circle will have the order 106 . The answer should be known with 10 - 5 precision. Roofly speaking, we need 11 digits, double precision will be enough.
. The center and the radius of the new circle will have the order 106 . The answer should be known with 10 - 5 precision. Roofly speaking, we need 11 digits, double precision will be enough.
Let the number in the end be N = 2k· 5m·(other primes). The number of zeroes at the end of N is equal to min(k, m). At the aid of dynamic programming find minimal value of k (let it be k1) and minimal value of m (let it be m1), and paths that lead to these values. In case of k1 < m1 choose the path corresponding to k1, else m1.
So min(k, m) is the upper bound for the answer. Let us prove that it is the lower bound too. If there exists a path leading to a number with number of zeroes less than min(k, m) then in the factorization of that number the power of two is k < k1 or the power of five is m < m1. We come to a contradiction.
So we need to calculate the power of 2 and 5 in the factorization of each value in the matrix and use dynamic programming on each of the two matrices.
In the case of matrix containing zeroes, calculate separately the best path not containing zeroes and any path containing zeroes:
Replace all 0 by 10 and use the method described above. For paths containing zeroes the result will contain at least one zero at the end. If the method returned a number without zeroes at the end, the corresponding path is the answer, else any path containing zeroes is the answer.
The complexity of the algorithm depends on the complexity of the dynamics, it is O(N· M).
At the first pass calculate the sum of points for each player at game end. Let M be the maximum of these sums. At the second pass check every round. If current player X has not less than M points and his final score is equal to M then he is the winner.
The following test illustrates that player could receive more than M points, then lose some and, finally, win.
Input:
Masha 12
Masha -5
Sasha 10
Masha 3
Output:
Masha
Problem С. Commentator problem
Let R be the distance from point А to a circle with center О and radius r. From this point the circle is observed at the angle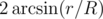 .
.So, the three stadiums are observed at the same angle if R1 / r1 = R2 / r2 = R3 / r3.
Take two different points A, B. The set of points C that AC / BC = const is either a line (perpendicular bisector of AB) or a circle with center somewhere on the line AB. This circle is easy to find. It contains two points that lie on AB and satisfy AC / BC condition.
Let X1 be the set of points from which stadiums 1 and 2 are observed at the same angle. Let X2 be the set of points from which stadiums 2 and 3 are observed at the same angle. The answer belongs to both X1 and X2 . The centers of the three stadiums don't lie on one line, so the number of points in the intersection of X1 and X2 will be finite.
Check them all. The answer is the point that lies closer to any of the stadiums. The stadiums don't intersect, so that point will not lie inside any of them.
How to get a big circle for X1 : put the centers of the stadiums in the points far away, for example in (0, 0) and (1000, 0). The ratio of the radii should be the closer possible to 1, for example
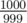 . The center and the radius of the new circle will have the order 106 . The answer should be known with 10 - 5 precision. Roofly speaking, we need 11 digits, double precision will be enough.
. The center and the radius of the new circle will have the order 106 . The answer should be known with 10 - 5 precision. Roofly speaking, we need 11 digits, double precision will be enough.Problem B. The least round way
Let us solve the problem in the case of positive matrix.Let the number in the end be N = 2k· 5m·(other primes). The number of zeroes at the end of N is equal to min(k, m). At the aid of dynamic programming find minimal value of k (let it be k1) and minimal value of m (let it be m1), and paths that lead to these values. In case of k1 < m1 choose the path corresponding to k1, else m1.
So min(k, m) is the upper bound for the answer. Let us prove that it is the lower bound too. If there exists a path leading to a number with number of zeroes less than min(k, m) then in the factorization of that number the power of two is k < k1 or the power of five is m < m1. We come to a contradiction.
So we need to calculate the power of 2 and 5 in the factorization of each value in the matrix and use dynamic programming on each of the two matrices.
In the case of matrix containing zeroes, calculate separately the best path not containing zeroes and any path containing zeroes:
Replace all 0 by 10 and use the method described above. For paths containing zeroes the result will contain at least one zero at the end. If the method returned a number without zeroes at the end, the corresponding path is the answer, else any path containing zeroes is the answer.
The complexity of the algorithm depends on the complexity of the dynamics, it is O(N· M).
Problem A. Winner
Simple problem, just code it.At the first pass calculate the sum of points for each player at game end. Let M be the maximum of these sums. At the second pass check every round. If current player X has not less than M points and his final score is equal to M then he is the winner.
The following test illustrates that player could receive more than M points, then lose some and, finally, win.
Input:
Masha 12
Masha -5
Sasha 10
Masha 3
Output:
Masha











task B, submission #3726143, I got:
Can I see what concrete input was in this test to find the reason? And who is Yuri? ))
There is one zero in the test — the best answer.
you saved hours of debugging. Thanks mate
could someone help me with the problem B, please ?
here's my code: http://ideone.com/1Juljl
thanks in advance :)
why didn't it appear in the recent actions? I need some help.
why problem B is O(n*m)? isn't it o(n*n)?
what is wrong with this solution http://codeforces.com/contest/2/submission/44454112
It fails in test 10.
Take a simple test:
Answer: b
[Solved]
In problem B if the input is
3
1 2 3
4 5 6
7 8 9
can one solution could be RRDD too?
Yes, I think so. Usually in the problem statement, it says "if there are more than one such path, print any possible path." I don't know why they didn't say it in this problem.
Problem A)
Failing test case 10 W.A Can anybody please help me ?
my submission link is here — https://codeforces.com/contest/2/submission/94976880