Author: Milesian
Tutorial
Solution
Author: liouzhou_101
Tutorial
Solution
Author: liouzhou_101
Tutorial
Solution
Author: Milesian
Tutorial
Solution
Author: Milesian
Tutorial
Solution
Author: liouzhou_101
Tutorial
Solution
1738G - Anti-Increasing Addicts
Author: antontrygubO_o
Tutorial
Solution
Author: liouzhou_101
Tutorial
Solution











Guys, i dont know about editorial (it is not ready yet) but it is possible to solve C in 1 if statement. Check my submission
UPD: Okay, same as in editorial but anyway... Feel free to ask any questions :)
Can you explain how you thought of it during the contest ??
Sure! At first lets say thet even numbers are "0" and odd numbers are "1" cause we care only about parity, right? Then i started implementing simple cases like: "1100", "111111", "10000", whatever, and asked myself "what if we gonna add/remove more 0s/1s?" After a while i realized that if Alice gonna use simple copy strategy, then she will always win if amount of 1s % 4 == 0. And then i tried to think about other remainders and came up with complete solution.
Sorry for my bad english btw, it is not my native lang :|
wonderful solution ,but can you please explain me why "(odd + 1) % 4 == 0)" this is independent of parity of 0's ??
Sorry for not answering for a long time.
Yes it is. When amount of odd numbers % 4 == 3 it means that Alice can take any odd number on her first move and then just copy Bobs move. This is simillar to case when odd % 4 == 0. Alice always gonna get odd number of 1's + 1 she already have after first move. Just try to implement some trivial exmaples like "111" and add some 0's to this. You'll see that this is actually works
Some codeforces lags below, nevermind
Sorry for not answering for a long time.
Yes it is. When amount of odd numbers % 4 == 3 it means that Alice can take any odd number on her first move and then just copy Bobs move. Just try to implement some trivial exmaples like "111" and add some 0's to this. You'll see that this is actually works
Fairly sure my submission can also be reduced to only 1 if statements since it also checks all conditions whereby alice wins then if all of those don't apply returns boris.
However your solution is more elegant since it entirely disregards the number of 0s (which is cool haha).
Also I've coded for like a combined 30 hours so don't bully me for my code haha, advice would be appreciated though (also I did't do this in competition, and have never tried a contest, how much time should this task have taken me?).
I strongly recommend you to participate in competitions. Rather, there is no point in not participating in them (except time issue ofc). It doesn't matter how much time you spend on a task, as long as you can solve it yourself. Actually it's the best way to improve in mu humble opinion. The next time you encounter a similar problem, you will solve it faster
can you please explain me why we are taking modulo with 4?
Just try to analyze some simple case.
For example "1111". It doesn't matter who goes first, Alice can always get an even number. Why so? because after one "cycle" of moves amount of odd numbers will decrease by 2 and Alice gonna get exactly 1. So, she needs even number of ones. two 1's multiplied by even number. That is why we are talking about modulo 4. Everything else can be deduced from this case
pov : you got wrong answer on test 5 or 36 in problem B :
I got wrong answer on test 11 though.
This def needs a fix
Why weak pretests for problem B?
Worst round
Something similar happened to me :(
Work out E in 30 minutes after the competition,and FST in problem B(QAQ).
My solution for E:
Firstly,consider a special case:there's no zero in array $$$a$$$.
We notice if we put a "partition" between $$$a[i],a[i+1]$$$,we must put a "partition" between $$$a[j],a[j+1]$$$ as well,where $$$(a[1]+...+a[i])=(a[j+1]+...+a[n])$$$ (except the "partition" in the middle).
In other words,the "partitions" are in pairs.So the answer is $$$2^{k},k$$$ is the number of pairs.
Now let's consider an array $$$a$$$ including zeros.
Remove all zeros from $$$a$$$,we get a new array $$$b$$$.
The same as the special case above,if we put a "partition" between $$$b[i],b[i+1]$$$,we must put a "partition" between $$$b[j],b[j+1]$$$ as well,where $$$(b[1]+...+b[i])=(b[j+1]+...+b[n])$$$.
Because there're zeros,the situaion is a bit more complex:
Assume there're $$$x$$$ zeros between $$$b[i],b[i+1]$$$ and $$$y$$$ zeros between $$$b[j],b[j+1]$$$,the number of plans to place "partitions" is:$$$ \Sigma^{min(x+1,y+1)}_{i=0}C^{x+1}_{i}C^{y+1}_{i}$$$.
Take care of boundary conditions:
-all numbers are zeros
-the array has zeros at both the beginning and the end
-the "partition" in the middle
:(
skip2004 's currently accepted submission for problem H seems to fail on Ticket 16227 from CF Stress.
Can someone hack it for me? or let me know if I constructed an invalid testcase? Thanks.
Good job! It's a pity that this case does not appear in system tests.
Is there a dp solution for C ? if yes please share
Added.
Can you please explain your intuition for C with DP? I did not even realize that this could also be solved with DP.
Intuition is that you can calculate if Alice can win or not in position of 1 even, 1 odd using position 0 even, 1 odd and 1 even, 0 odd. dpAlice[i][j] = !dpBob[i-1][j] || !dpBob[i][j-1] and some other logic.
the states of the game are of the form (howManyEvensLeft, howManyOddsLeft, Alice's current sum's parity, whoseTurnIsIt). from this you could write a recursive function and add memoization (thank god n is only 100 lol)
i saw you code in bob's turn u have written (p1+p2)==0 then return A%2==1. but at the end of numbers isn't it like alice should have even sum otherwise she looses so after the end even if it's bob's turn shouldn't it be return A%2==0. i don't understand why this code is correct
Could you please explain the
z+y+1in the code?I am not 100% sure, but here are my thoughts. This DP solution was not very intuitive for me but it is clever so if liouzhou_101 can correct me.
dp[x][y][z] gives whether Alice or Bob at a particular stage of game can get even/odd parity (z = 0 or 1) from x even and y odd numbers.
Where x is the current count of even numbers, y is the current count of odd numbers remaining in list
Note that when y is even parity of (z+y+1)%2 changes when moving from Alice to Bob or vice-versa.
and when y is odd parity of (z+y+1)%2 remains the same when moving from Alice to Bob or vice-versa.
Now in the recursion when moving from Alice->Bob or Bob->Alice we have cases
Cases for Alice->Bob include
Case 1: y is odd and Alice wants even parity from remaining moves.
Bob will try to defeat Alice by taking even parity sum from remaining numbers. Hence Bob will want even parity. So parity remains same from Alice to Bob.
Case 2: y is odd and Alice wants odd parity from remaining moves.
Bob will try to defeat Alice by taking odd parity sum from remaining numbers leaving only even parity sum for Alice. Hence Bob wants odd parity, same as Alice.
Case 3: y is even and Alice wants even parity sum from remaining moves.
So Bob will take odd parity sum from remaining moves. We can see parity switches from Alice to Bob.
Case 4: y is even and Alice wants odd parity sum from remaining moves,
So Bob will take even parity sum from remaining numbers. Again, parity switches from Alice to Bob.
So we can see when odd count of odd numbers is there, parity stays same. But if even count, parity switches from 0 to 1 or 1 to 0. The same logic is there for Bob to Alice.
so parity switch in recursion is defined as
z' = (z+y+1)%2leetcode07 ayush002024 lbm364dl if it helps.
Thank you. I understood it. To sum up, in general say you want parity $$$z$$$, and the total parity is $$$y$$$. To achieve this, the other player should get parity $$$y - z \equiv z + y \mod 2$$$, so if they don't want you to achieve your goal, they should try to get the opposite parity, which is $$$z + y + 1$$$.
What's wrong with my solution for problem A?
solution
Try
I didn't realize that D was supposed to be a graph problem, and I think the problem can be simplified a lot. Basically, the original (unknown) array $$$a$$$ can be partitioned into subarrays that alternate between $$$\leq k$$$ and $$$> k$$$. For each element in a given subarray, the value it generates in the result is always the last element of the previous subarray. The only exception is the first subarray, which always generates either $$$0$$$ or $$$n + 1$$$, depending on whether it is $$$\leq k$$$ or $$$> k$$$ respectively.
So what I did was build a 2D vector, where $$$ind[i]$$$ stores all of the indices of $$$b$$$ that contain the value of $$$i$$$. Then each $$$ind[i]$$$ actually represents an entire subarray of the unknown $$$a$$$. The first subarray is either $$$ind[0]$$$ or $$$ind[n + 1]$$$ (exactly one will be non-empty). Given the elements of a subarray, exactly one element (the one that appears last in $$$a$$$) will be generated by the next subarray while the remaining elements (if any) will not be generated at all. So we can check each element of the current subarray to find which element $$$x$$$ has $$$ind[x]$$$ as non-empty. Then we need to ensure that $$$x$$$ is added last from this subarray, and then move to the next subarray, which is $$$ind[x]$$$. Repeat until we reconstruct the entire original array.
As for finding $$$k$$$, we can add elements from the $$$\leq k$$$ subarrays to a set. We can identify whether the first subarray is a $$$\leq k$$$ subarray (if it's $$$ind[0]$$$) or a $$$> k$$$ subarray (if it's $$$ind[n + 1]$$$) and then it simply alternates. The value of $$$k$$$ is the largest element in this set at the end.
My Submission: 174151773
It's possible that what I just described is actually identical to the graph approach (where this 2-dimensional vector is the adjacency list?), but I don't think any graph knowledge is necessary at all to easily solve this problem. At the very least, I think this is easier than either the $$$O(1)$$$ or the DP solutions for C...
I did exactly the same!
terrible pretests for B, what is this trend of skipping common edge cases in pretests?
Indeed, no matter whether you believe or not, we didn't realize why many people were hacked. We tried to list every kind of generator in pretests. But even some final tests were provided by real hackings you know?
the most common fst was not considering first index of prefix sum array being negative, did u guys really forget to include that basic edge case in pretest?
No, actually, I think. The system already noticed us all boundary cases were contained by automatically checking.
no, that case was main test 36 which is not in pretests, you can code a solution ignoring s[0] being negative and check if u want
To be honest, that comes from hack. My bad.
:(
Pretest 2 didn't have any negative numbers; that was the main reason why there were hacks.
Here's my solution to G. I think it's somewhat similar to the editorial. It looks long and complicated, but I've tried to thoroughly explain the motivation behind it, the central idea is fairly straightforward, and I think all the steps are pretty intuitive. I hope it can help anyone confused by the main editorial.
First, notice that the problem doesn't change if we start with an empty grid and place down cells, where we are forced to place cells in grid spots marked
0.For now, ignore the constraints on which cells need to be filled. Let's start by considering when $$$k = 2$$$. The most obvious solution would be something like this:
If you play around with it a bit, you'll notice you can "twist" the path around, and that actually, any path from the bottom left to the top right works.
This motivates looking at the diagonals which go from the top left to the bottom left (or more formally, sets of cells with the same value of $$$r - c$$$), since at each step going up or right, we move into a new diagonal (In this next picture, the distinct diagonals we're considering are marked with different letters).
It's easy to show that there can be at most $$$k-1$$$ cells in one diagonal (otherwise, there would be a sequence of size $$$k$$$ going down and right).
A natural question to ask is, what's the maximum number of cells we can place down under this constraint? Well, notice that the number of cells in each diagonal is $$$1, 2, \ldots, n - 1, n, n - 1, \ldots, 2, 1$$$. So there are $$$2k-2$$$ diagonals where we can fill every cell (the diagonals with $$$\leq k - 1$$$ cells), and a remaining $$$2n - 1 - (2k - 2)$$$ diagonals where we can only place $$$k-1$$$ cells. Doing the algebra gives:
$
If you think of this expression as the number of cells in 2 $$$n \times (k-1)$$$ rectangles, minus one $$$(k-1)\times(k-1)$$$ square, it's not hard to see that this is precisely equal to $$$n^2 - (n-(k-1))^2$$$: the number of cells we want to remain (if you want, you can do the algebra to convince yourself). So, the maximum number of cells we can place down is exactly equal to the number of cells we need to place down!
So we know that in diagonals with $$$\leq k - 1$$$ cells, every single cell needs to be filled. Example with $$$n = 5, k = 4$$$:
Let's call these forced cells.
What about all the other cells? Well, we know that all the other diagonals must have exactly $$$k-1$$$ cells. Let's keep playing around with the problem, and try to find solutions for different $$$k$$$.
If you try to construct some solutions, after a while, you'll notice that all the solutions you find are composed of $$$k-1$$$ disjoint paths going from the lower-left forced cells to the top-right forced cells. For example, with $$$n=5,k = 3$$$:
Here, the forced cells are marked
Fand the paths are markedXandY. It's also important to note that these paths never go down or left: always right or up.Let's try to show that this $$$k-1$$$ paths idea is necessary and sufficient for a solution.
We can do this with a kind of induction. We start with the lower-left diagonal, and build up $$$k-1$$$ paths.
Base case: let's look at the diagonal immediately adjacent to the last forced diagonal in the lower-left. Here's a picture for $$$n = 5, k = 4$$$:
The cells we're interested in are marked with
!s. Recall that we need to have exactly $$$k-1$$$ cells in this diagonal. It's easy to see that no matter how we place these $$$k-1$$$ cells, they will form the starting points of $$$k-1$$$ disjoint paths.Induction step: if we have $$$k-1$$$ paths leading up to some diagonal, it is necessary to extend these $$$k-1$$$ paths into the next diagonal. This part's harder to make pictures for, so bear with me.
Let's say we want to add a cell in the new diagonal such that it isn't adjacent to any cells in the previous diagonal. This is the only way to not extend the $$$k-1$$$ paths.
Let's try and make the leftmost cell (we'll denote it $$$(r, c)$$$) in the diagonal not adjacent to any cells in the last diagonal. Then, there are 2 cases:
Notice that if neither of these conditions hold, then $$$(r, c)$$$ must be adjacent to the leftmost cell in the previous diagonal.
OK, so we're forced to extend the leftmost path. What about the next one (the second-to-the-left cell in the new diagonal)? Similar reasoning will show that this case is also impossible, and extending the reasoning, that we are forced to extend all of the $$$k-1$$$ paths. So, the $$$k-1$$$ paths are necessary for the solution.
Suppose that we have $$$k-1$$$ paths going up and right. Let's try to construct a sequence of $$$k$$$ cells going strictly right and down.
By the pigeonhole principle, there must be at least one path that has at least 2 of its cells in this sequence. But this is impossible: if there were two cells $$$(r_1, c_1), (r_2, c_2)$$$ in one of these paths such that $$$r_1 < r_2$$$ and $$$c_1 < c_2$$$, then it would be impossible to get from one of these cells to another going only right and up! So they couldn't possibly be a part of the same path.
And so, if we have $$$k-1$$$ paths, it is impossible to construct a sequence of $$$k$$$ cells going strictly right and down.
Alright! So now all we need is to implement it.
Let's build our paths, starting from the rightmost one. For convenience, we'll put the starting points of our paths in the last forced diagonal in the lower right corner. For example, with $$$k = 4$$$, it would look like this (
Fdenotes a forced cell,Sdenotes the starting point of a path):It's not hard to see that any placement of $$$k-1$$$ cells in the first non-forced diagonal can be achieved by starting our paths like this.
Now, let's build the actual paths. This is where the constraints on which cells we must place come in. Suppose that the endpoint of our path is currently at $$$(r, c)$$$. Let's look for points where we need to place down a cell (in other words, that are marked $$$s[i][j] = 0$$$ in the input), that are in the same row as our path and to the right of it. We extend our the path to the right to cover all these cells. Then, when there are none left, we move up to row $$$r-1$$$. Note that if some cell has already been covered by a previous path, we should ignore it.
This greedy idea works because the paths are disjoint ~--- if we didn't go to the right to collect these cells, then some path starting to the left of the current path would have to cross over and collect them, and avoiding this happening can't make our solution worse.
In this way, we greedily build our paths. At the end, if there is any cell that needs to be covered that we haven't covered, then our answer is
NO. Otherwise we can outputYESand our construction. So are we done?Not quite. There's still a possibility that the paths intersect at the very top, and that we haven't actually placed down enough cells. There's an easy fix, though. Iterate through the diagonals from bottom-left to top-right. If there are less than $$$k-1$$$ cells in this diagonal, then we place down cells (iterating left to right) in empty spots that are adjacent to cells in the previous diagonal, until we get to $$$k-1$$$ cells.
Notice that since there are exactly $$$k-1$$$ cells in the previous diagonal, there must be at least $$$k-1$$$ cells in this diagonal adjacent to a cell in the previous diagonal. So we can always place down enough.
The proof that this preserves the paths is a bit harder to justify. Intuitively, if two paths ever intersect, then they must be mashed together into the leftmost part of the diagonal, and adding cells to the right gives the mashed together paths a new cell to move into.
My AC code: 174160936
Video editorial of Problem D.
It is stupid that people so heavily downvote the editorial when their complain is not about the editorial
Seems that people have complaints about FSTs, but If every solution passing pretests will also pass system tests, what is the purpose of pretests and system tests after all?
system tests is just to ensure that some heurestics which is not the actual solution doesnt pass, it doesnt mean that edge cases which really should be in the pretests get missed out. Checking logic is more important than the ability to code edge cases
I lost my GM account after the contest, for I didn't got F correct after some wrong attempts.
Very sad :(
Can someone see what went wrong in my DP solution in C? 174187246
Here is an example test case:
The answer should be "Alice", not "Bob".
When you initialized your DP, you set
dp[2][1][1]to be false. However, if Alice picks the (only) even number, Bob has no choice but to pick an odd number, allowing Alice to take the other odd number and secure the odd sum as desired.Note: there might be other mistakes, but this is the one I found that explains the issue with this particular test case.
Thank you! My code got accepted after changing dp[2][1][1] to true; that was a bit silly of me, could have gotten (back) to specialist if I AC'd that problem
It's unfortunate that you missed it in the contest, but at least it works now!
To be honest, there was no need to hardcode cases where an index is equal to 2. The furthest back that you check is with indices $$$i - 2$$$ or $$$j - 2$$$, so as long as you correctly initialize the cases where the index is $$$0$$$ or $$$1$$$, it should have been fine to build the DP from indices 2 onwards.
That's fair too, but previously I had a different DP method where I would need to hardcode this. After figuring out (and implementing) the correct solution I thought that "it wouldn't hurt to just leave the base cases like this, right?", and damn I was wrong, it hurts
Really funny that I went overkill and did DP on C. Well an AC is an AC, I highly appreciate the low contraints though
Thanks for understanding! That's also why I set low contraints to this problem.
Personally, I still think the DP approach is much easier than the case analysis, since I don't think it is obvious at all as to what the optimal strategy is in each of these cases, or even to figure out that considering the number of odds modulo 4 suffices to characterize most cases. Either way, I think it's a good problem, and it's nice that both approaches are accepted.
Yes, that's what I wanted, both approaches are accepted.
I did DP as well but I was reading the input without taking the absolute value modulo 2. Therefore I failed miserably while the DP was correct lol. Rating dropped hard this contest. I also believe DP was more straightforward than the O(1) solution, good thing they kept the input small. After the contest I sadly submitted a correct solution.
174190808
I only do this absolute value modulo trick in first several problems, aiming at pointing out something that you might not take care of.
I'm more happy to see you guys really learned something from this problem, rather than getting fake and useless contributions from announcement.
Best luck!
Yeah, I'll surely double check the constraints from now on. Many times going slow but steady is better.
tbh, allowing the values to be negative in a problem where you need to check parity is kinda a jerk move, especially since it unfairly punishes those who happened to carelessly check if mod 2 is equal to 1, whereas those who carelessly checked if mod 2 is equal to 0 (like myself, actually) are unaffected.
By the way, you probably already know this, but although it's okay to take the absolute value modulo 2, this would not work with a larger modulo, e.g., -4 mod 3 should actually be 2 (C++ gives -1, so you need to add 3), but applying the absolute value first would yield 1, which is incorrect.
Beginner friendly dynamic programming solution using memoization for 1738C - Even Number Addicts.
174190808
\begin{equation} solve(o, e, w, a)= \begin{cases} w & \text{if } o = 0 \ \text{&} \ e = 0\\ max \{solve(o-1, e, !w, false), \ solve(o, e-1, w, false)\}& \text{if } \text{alice's turn} \\ min \{solve(o-1, e, w, true), \ solve(o, e-1, w, true)\} & \text{if } \text{bob's turn} \end{cases} \end{equation}
In the equation above, o represents the amount of odd numbers, e represents the amount of even numbers, w is the boolean variable that tells us if alice is winning and finally, a is another boolean variable tha tells us whose turn it is. Of course we are also using memoization to not re-calculate sub-problems. Complexity is $$$O(n^2)$$$, the size of the memoization table.
That's why I set low constraints. Hope you guys not only know case works but basic DP ideas.
This is the clearest and most intuitive solution that I have seen.
clearest explaination
Can someone explain the dp approach to problem c?
Let
dp[i][j][k = 0/1]be whether A can always get parity k with i odds and j evens. You can see that a move is considered winning if no matter what parity B chooses in the next move, A always have a way to win. Say if A chooses an odd number, it's a winning move if A can always win even if B chooses an odd number or an even number.Consider
dp[i][j][k]:Case 1: A chooses an odd number, B chooses an odd number. This is winning if A can always get an opposite parity of k with i-2 odds and j evens, hence
dp[i-2][j][1-k].Case 2: A chooses an odd number, B chooses an even number. This is winning if A can always get an opposite parity of k with i-1 odds and j-1 evens, hence
dp[i-1][j-1][1-k].You can see that if A chooses an odd number, it's considered winning if
dp[i-2][j][1-k]anddp[i-1][j-1][1-k]are both true.Case 3: A chooses an even number, B chooses an even number. This is winning if A can always get the same parity with i odds and j-2 evens, hence
dp[i][j-2][k].Case 4: A chooses an even number, B chooses an odd number. This is winning if A can always get the same parity with i-1 odds and j-1 evens, hence
dp[i-1][j-1][k].Using the same logic, you can see that A choosing an even is winning if and only if
dp[i][j-2][k]anddp[i-1][j-1][k]are both true.Hence we get this dp formula:
dp[i][j][k] = (dp[i-2][j][1-k] && dp[i-1][j-1][1-k]) || (dp[i][j-2][k] && dp[i-1][j-1][k]), and the answer of the problem is
dp[x][y][0], where x is the number of odd numbers, and y is the number of even numbers in the array.Small note: if j < 2, then we consider
dp[i][j-2][k]to be true (since it's not possible to have that particular sequence of moves), and it's the same for the others.Example solution: 174190925
Man! I have been wracking my head over this but this is the only explanation that made sense to me.
For F,I can't quite understand why we should choose an unvisited vertex u "with the largest degree" ? Can someone help me?
I think the way it tones down is that we need to find all the connected components and then we can color all the elements in one connected component in the same color. ( because then s_c <= n_c^2 will always hold)
If you dont visit the vertex with the maximum degree you might not find the connected components correctly, take for example the image attached below
If you start with lets say the smallest degree, you will find the connected components as follows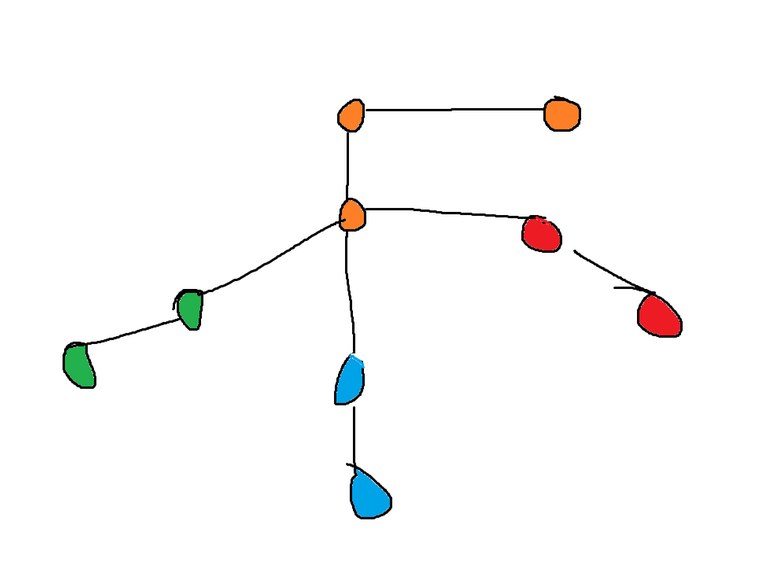
If you are confused why its colored like this, then lets say you start with 1 degree vertices you color them and their adjacent 2 degree vertices. Now you pick the 2nd degree vertices (lets say you take the orange one), you look to its right and you see the 1 degree vertex which is already visited, so you will break and not discover the middle vertex ( with 4 degree)
But if you explore the maximum degree vertex first, you will end up like this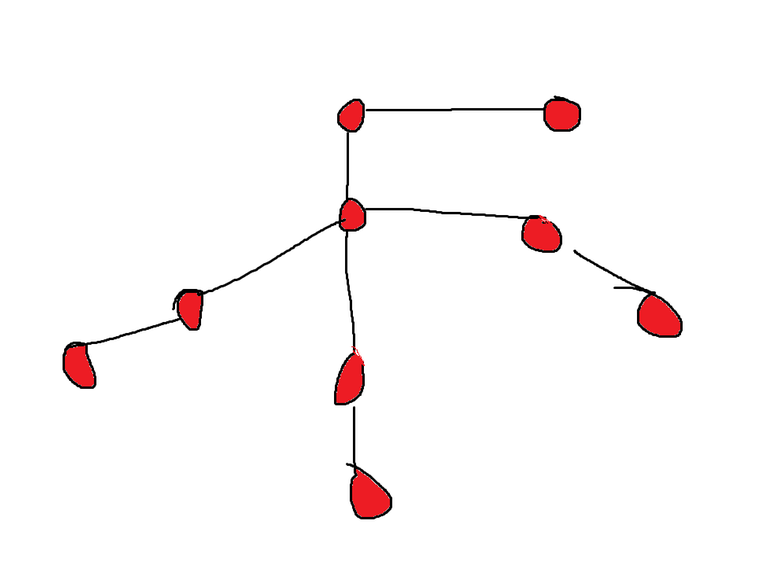
!Thank you very much for your splendid answer!!!
hey my personal opinion but both B and C had unnecessary negative numbers, generally when giving questions involving performing division or modulus, not giving negative numbers is a good idea due to weird stuff in compilers where -1 %2 evaluates to -1. Luckily i didnt get affected in C (did in B) but overall it shouldn't be about who remembers how compilers calculate negative values which causes the difference between a AC and WA
Some of the problems are bad.
Problem B:Just a template problem.
Problem C:Why just let n<=100 ???
Problem H:You can find the problem which is even harder than this problem.
It was my first contest. I could only solve 1, what is the rating of the first problem?
It is still unknown. Usually, few days after the contest the problems get rated.
Okay thanks
Hey Vito, could you please tell me the difficulty of Codeforces round. Are global rounds comparatively tougher than div3, div4 or equivalent to div2 or div1 ?
Let's say $$$f(x)$$$ is difficulty of Div.$$$x$$$ contest. $$$f(4)$$$ $$$<$$$ $$$f(3)$$$ $$$<$$$ $$$f(2)$$$ $$$<$$$ $$$f(1)$$$.
In Global rounds there are more problems than in normal Div.2 or Div.1 round. The first few problems are of similar difficulty as typical Div.2 round first few problems. Last few problems in the problemset are usually harder than any Div.2 problems.
Great!
Can anyone help me find what's wrong in my solution 174220349 for Problem C?
Dear abhinav_99, you should replace if(a[i] % 2 == 1) with if(a[i] % 2).
In C99 it is guaranteed that:
if B != 0{ if A < 0 then A % B <= 0 if A > 0 then A % B >= 0 if A == 0 then A % B == 0. }
After several contests, I found that when failing because of a wrong answer on test >=3, it is always some mild but annoying bugs, because you have already passed many big tests.
POV: you are rainboy
Weirdest thing is happening for my submission for A. I submitted my code during the contest and got TLE and left it at that, but when I optimized the code multiple times I was still getting TLE, so I went and checked the submissions of others and copied and pasted it(because I had written exactly the same code as that solution) and I am still getting TLE for some reason.
My Copied Submission
Original Submission by CF user
Why is this happening??
edit : I am also doing the same thing as editorial.
You're using PyPy 3 not Python 3. Does that make a difference? (I have no idea!)
It worked!!
Wow, I didn't know that PyPy3 and Python 3 would make this much difference. Also when I changed it from PyPy3 to Python 3.x.x it said below that PyPy is usually faster.
This is the first time I used Python 3 during submission as well.
Thanks a lot of pointing it out!!!
In PyPy, input and/or output is slower. Adding the following 2 lines of code at the beginning makes your TLE code work in 280 ms:
What is wrong with my submission for problem B? (174286190) Everything seems correct to me...
It's just 5 lines of code
c problem,I can't find why is not passed test3?help help me 174499898
In the testcases where x is negative and odd,x%2 will be -1 but not 1
For Proble-C, can someone point out an error in my DP solution — 174134613. Thank you.
Take a look at Ticket 16245 from CF Stress for a counter example.
Thanks a lot! I made an error in writing a base case. I made sure to check the base cases like 4-5 times during the content... can't belive I did such a horrible mistake...
Btw, what is this CF Stress?? It seemed interesting
cfstress.com is a website I've created that helps you find the smallest counter example for all upcoming problems on Codeforces. You can be as specific as you want, for example
and it'd give you back a counter example if it exists. All you need to do is provide your submission ID.
But of course, it's not free to use.
What an excellent problem C! It brought me back to the my junior-high school time!
UPD : understood the mistake.
I think this D is so difficulty but why it is only 1900?!
why such a big editorial of D!! My solution was just simple topological sort
DP For C:
even-count of even numbers remaining.
odd -count of odd numbers remaining.
a_coins- current parity of coins at Alice(we consider this since win or lose only depend on parity of coins at Alice).
who : who is moving now(1-Alice move, 0-Bob move).
state:
(even,odd,a_coins,who)
what does rec(state) return?
can Alice win from the current state? that is from the current state, can we reach a state where we have no coins left, i.e., no more moves can be played(base case) with a_coins parity even?
Base Case:
if(even==0 && odd==0) return a_coins==0
Transitions:
if(who==1)Alice's move:
if any of rec(even-1,odd,a_coins,0) or rec(even,odd-1,1-a_coins,0) is winning for Alice then Alice will choose it. Parity is changed when Alice Moves and takes the odd coin
if(who==0)Bob's move:
if both rec(even-1,odd,a_coins,1) and rec(even,odd-1,a_coins,1) must be winning else Bob will choose to push Alice to losing state.
Answer:
rec(0,0,0,1) having no coins initially is even parity so a_coins=0
211099131
Update: sorry question is irrelevant now as I had misunderstood that pop in problem H is pop back not pop front, my bad...
Can someone help with a submission for B. got wrong ans for tc5.
sub id: 256240098
include <bits/stdc++.h>
using namespace std;
define fast ios_base::sync_with_stdio(false);cin.tie(0);cout.tie(0)
define ll long long
define ld long double
define all(a) a.begin(), a.end()
define f(i,s,e) for(ll i=s;i<e;i++)
define yes cout<<"YES\n";
define no cout<<"NO\n";
bool check(vector v){ ll n = v.size(); f(i,0,n-1){ if (v[i]>v[i+1]) return false; } return true; }
signed main(){
while(t--){
ll n,k; cin>>n>>k; vector<ll> v(k); f(i,0,k) cin>>v[i]; vector<ll> ans; if(n==k){ ans.push_back(v[0]); f(i,1,k){ ans.push_back(v[i]-v[i-1]); } } else{ ll diff = n-k; if(diff + 1 <= abs(v[0])) { if(v[0]>0){ f(i,0,diff) ans.push_back(1); ans.push_back(v[0]-diff); } else{ f(i,0,diff) ans.push_back(-1); ans.push_back(v[0]+diff); } sort(all(ans)); } else{ if(v[0]>0){ f(i,0,v[0]) ans.push_back(1); f(i,0,diff+1-v[0])ans.push_back(0); } else{ f(i,0,-v[0]) ans.push_back(-1); f(i,0,diff+1+v[0])ans.push_back(0); } sort(all(ans)); } f(i,1,k){ ans.push_back(v[i]-v[i-1]); } } if(check(ans)) yes else no} return 0; }