I'm learning number theory and I cannot figure out the solution of following problem:
Given an array of integer A with N element with constrains N <= 10^5, A[i] <= 10^12. We call GCD(L, R) is greatest common divisor of all element A[L], A[L + 1], ..., A[R]. Return the sum of all contiguous sub-sequence in A.
I did have some idea that, for fixed index i, the value of GCD(i, j) will be decreasing as GCD(i, j) >= GCD(i, j + 1). Also, because GCD(i, j + 1) must be equal or divisor of GCD(i, j), the number of distinct value X of GCD(i, j), GCD(i, j + 1), ..., GCD(i, N) will satisfies 2^X <= A[i].
But I cannot go further. Please give me some more insights.










Yes, for every
iGCD decreases at mostlg(A[i])times. If you could calculateGCD(i,r)for any fixedrfast enough, then you could find all the positions where GCD changes using binary search.Thank you very much. Value
GCD(i,r)can be computed by using Segment Tree inLog2(N), but I found that forN = 1e5and large A[i] it somehow still slow. Is there any more efficient method for query operation? Currently it looks like that:You can use RMQ, but instead of min/max use gcd. Queries can be answered with only one gcd call. Make sure to use a fast gcd implementation.
you can compute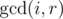 in
in 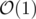 using Sparse Table data structure (instead of Segment Tree).
using Sparse Table data structure (instead of Segment Tree).
Thank mukel and JuanMata a lot, I implemented RMQ with Sparse Table with the help of tutorial in TopCoder and it works much more efficiently than Segment Tree! I actually learned several new techniques :D
I came across a similar question recently in which I have to find the sum of GCD's of all subarrays.
I know that GCD decreases at most log(A[i]) times so I can find all the positions where GCD decrease using Binary Search and sparse table but I am unable to think that how should I find the sum of GCD's of all subarrays from range L to R.
My approach is O(nlogn) for a single query, can it be done faster and more efficiently if there are multiple queries?
ex- A = [2,3,4,5]
L = 1, R = 4 (1-indexed)
ans = 20.
This problem is from an ongoing contest.
Which contest was that? Can you please share a link?
HackerEarth circuits which happened 2 weeks ago.
Thanks a lot! It's a great problem by the way!
Yeah ! my idea is mostly the same as discussed above. And here my code goes -->
https://ide.codingblocks.com/s/135466
Although i have added comments to make my code readable.
A similiar problem on Codeforces.
Can you please share the problem source?
Will you explain me the solution of above problem?
Sorry for late reply,
We don't need any complicated data structure to solve this problem
The only observation we need is that the number of distinct gcd values ending
at a given index is atmost log(n), so we can maintain a map that tells us all
the distinct gcds that have ended in the previous index, using this we calculate
all the new gcds and also update the map simultaneously
Submission link:https://codeforces.com/contest/475/submission/250578491
Also please share any different approach that you may have learnt of during this time