Мои попытки ускорить куб до O(1)

№	Пользователь	Рейтинг
1	ecnerwala	3648
2	Benq	3580
3	orzdevinwang	3570
4	cnnfls_csy	3569
5	Geothermal	3568
6	tourist	3565
7	maroonrk	3530
8	Radewoosh	3520
9	Um_nik	3481
10	jiangly	3467

№	Пользователь	Вклад
1	maomao90	174
2	adamant	164
2	awoo	164
4	TheScrasse	160
5	nor	159
6	maroonrk	156
7	-is-this-fft-	150
8	SecondThread	147
9	orz	146
10	pajenegod	145

Всем привет. Недавно мне в голову пришла следующая задача: Рассмотрим множество точек (x, y) с целыми координатами таких, что 0 <= x < a и 0 <= y < b. Требуется найти количество остроугольных треугольников с вершинами в этих точках.

Попытки проинтерполировать

Ясно, что можно написать функцию f(a, b), которая будет искать ответ и работать при этом за (ab) ^ 3. Я предположил, что она ведет себя как многочлен от двух переменных степени не более 6. Я попытался её проинтерполировать, используя эту теорему. Но у меня ничего не получилось, так как при мономах степени больше 6 интерполяция давала ненулевой коэффициент. Не получилось также с тупоугольными и прямоугольными треугольниками.

code (для прямоугольных треугольников)

int stupid(int a, int b)
{
    int ans = 0;
    for (int x1=0;x1<a;x1++)
        for (int x2=0;x2<a;x2++)
            for (int x3=0;x3<a;x3++)
                for (int y1=0;y1<b;y1++)
                    for (int y2=0;y2<b;y2++)
                        for (int y3=0;y3<b;y3++)
                        {
                            int a = (x1 - x2) * (x1 - x2) + (y1 - y2) * (y1 - y2);
                            int b = (x1 - x3) * (x1 - x3) + (y1 - y3) * (y1 - y3);
                            int c = (x3 - x2) * (x3 - x2) + (y3 - y2) * (y3 - y2);
                            if ((a + b == c) && min(a, min(b, c))) ans++;
                        } 
    return ans / 2;
}
signed main()
{
    int C1 = 5, C2 = 5;
    ld res = 0;
    for (int a1=4;a1<=C1+3;a1++)
    {
    	for (int a2=4;a2<=C2+3;a2++)
    	{
    		int d = 1;
    		for (int ai=4;ai<=C1+3;ai++) if (ai != a1) d *= a1 - ai;
    		for (int ai=4;ai<=C2+3;ai++) if (ai != a2) d *= a2 - ai;
    		res += (ld)(stupid(a1, a2)) / d;
    	}
    }
    cout << setprecision(20) << fixed << res;
}

Данный код узнаёт коэффициент при мономе a ^ (C1 - 1) * b ^ (C2 - 1)

Что я хотел бы узнать:

решается ли эта задача быстрее, чем за куб
решается ли эта задача за O(1)
может, кто-нибудь знает задачи, где формула для ответа не очевидна и её можно подобрать этим методом?

UPD: найдена формула для количества прямоугольных треугольников с b = 2: f(a, 2) = 2 * a ^ 2 - 4, a > 1.

UPD2: большое спасибо bronze_coder за нахождение решения за O(1) для b = const: OEIS A189814.

Для интерполяции надо использовать ai > b ^ 2. EDIT: ai > (b - 1) ^ 2

UPD3: Наконец, я написал решение за O((ab) ^ 2).

Code

int fast(int a, int b)
{
    int ans = 0;
    for (int a1=-a+1;a1<=a-1;a1++)
    {
	for (int b1=-b+1;b1<=b-1;b1++)
	{
       	    if (a1 == 0 && b1 == 0) continue; 
       	    for (int a2=-a+1;a2<=a-1;a2++)
	    {
	        for (int b2=-b+1;b2<=b-1;b2++)
		{
		    if (a2 == 0 && b2 == 0) continue;

		    // первое условие - скалярное произведение равно 0
		    // второе условие - векторное произведение < 0 - чтобы не считать одну пару дважды
		    if (b1 * b2 + a1 * a2 == 0 && a1 * b2 - b1 * a2 < 0)
		    {
		        int cnta = a - max(max(abs(a1), abs(a2)), abs(a1 - a2));
		        int cntb = b - max(max(abs(b1), abs(b2)), abs(b1 - b2));
		        if (cnta > 0 && cntb > 0) ans += cnta * cntb;
		    }
	        }
	    }
        }
    }
    return ans;
}

Теперь я могу использовать большие значения a и b для интерполяции.

Но всё равно кажется странным, что количество прямоугольных треугольников пропорционально (ab) ^ 2, а не (ab) ^ 3. Сейчас попробую понять, почему формула не работает для ai <= b ^ 2. EDIT: ai <= (b - 1) ^ 2

UPD4: Код, который находит формулу для f(a, b) при a > b ^ 2 и работает за O(b ^ 6):

Спойлер

int fast(int a, int b)
{
    int ans = 0;
    for (int a1=-a+1;a1<=a-1;a1++)
	for (int b1=-b+1;b1<=b-1;b1++)
	{
       	    if (a1 == 0 && b1 == 0) continue; 
	    for (int a2=-a+1;a2<=a-1;a2++)
	        for (int b2=-b+1;b2<=b-1;b2++)
		{
		    if (a2 == 0 && b2 == 0) continue;
		    if (b1 * b2 + a1 * a2 == 0 && a1 * b2 - b1 * a2 < 0)
		    {
		        int cnta = a - max(max(abs(a1), abs(a2)), abs(a1 - a2));
			int cntb = b - max(max(abs(b1), abs(b2)), abs(b1 - b2));
			if (cnta > 0 && cntb > 0) ans += cnta * cntb;
		    }
	        }
	}
    return ans;
}
struct polynom
{
    int x0 = 0, x1 = 0, x2 = 0;
    void print()
    {
	cout << x2 << "x^2 + " << x1 << "x - " << -x0 << endl;
    }
    ld get(ld x)
    {
	return x2 * x * x + x1 * x + x0;
    }
};
void interpolate(int b)
{
    polynom P = {0, 0, 0};
    vector<int> A = {b * b + 1, b * b + 2, b * b + 3};
    ld res = 0;
    vector<ld> B = {fast(A[0], b), fast(A[1], b), fast(A[2], b)};
    for (int i=0;i<3;i++)
    {
	int d = 1;
	for (int j=0;j<3;j++) if (A[i] != A[j]) d *= A[i] - A[j];
	res += (B[i] - P.get(A[i])) / d;
    }
    P.x2 = res;
    res = 0;
    A.pop_back();
    for (int i=0;i<2;i++)
    {
	int d = 1;
	for (int j=0;j<2;j++) if (A[i] != A[j]) d *= A[i] - A[j];
	res += (B[i] - P.get(A[i])) / d;
    }
    P.x1 = res;
    P.x0 = B[0] - P.get(A[0]);
    P.print();
}

Пытаясь найти закономерность в коэффициентах многочлена P, я обратился к OEIS, но ничего там не нашел :(, кроме x2 = b * (b - 1), что и так было очевидно.

UPD5:

Наконец-то нашёл формулу и решение за `O(min(a, b) ^ 6)`

Если a < b, то поменяем их местами. Теперь нужно решить за O(b ^ 6). Если a <= (b - 1) ^ 2 + 1, то запустим решение за O((ab) ^ 3) = O(b ^ 6). Теперь нужно разобраться с большими a.

Определения

Рассмотрим все прямоугольные треугольники и разделим их на 3 типа:

треугольники, у которых нет вершин на прямой x = a - 1
треугольники, у которых есть вершины на прямой x = a - 1 и две стороны параллельны осям координат
остальные треугольники

Обозначим количество треугольников третьего типа за C(a) (какая-то функция от a).

Количество треугольников второго типа можно посчитать по формуле (a - 1) * b * (b - 1) / 2 * 4:

Доказательство

Из определения следует, что для вершин (x, y) треугольников первого типа выполняется 0 <= x < a - 1 и 0 <= y < b, то есть их количество равно f(a - 1, b), по определению функции f.

Итак, f(a, b) = f(a - 1, b) + (a - 1) * b * (b - 1) / 2 * 4 + C(a)

Теперь докажем, что C(a) при всех a > (b - 1) ^ 2 + 1 — константа.

Доказательство

Лемма. Максимальный модуль разности абсцисс вершин треугольника третьего типа не превосходит (b - 1) ^ 2 + 1

Для доказательства посмотрим на рисунок.

Прикрепился только повёрнутый(

У нашего треугольника есть хотя бы две стороны, непараллельные осям координат. Пусть они AB и BC. Пусть угловой коэффициент прямой AB равен k, тогда у прямой BC он равен -1/k. Тогда разность абсцисс верши A и C не больше, чем (b - 1) / |k| + (b - 1) / |-1/k| = (b - 1) * (|k| + 1 / |k|).

Известно, что если мы возьмём два положительных числа и будем их сближать на числовой прямой с сохранением произведения, то их сумма будет уменьшаться. Тогда для максимизации |k| + 1 / |k| нужно минимизировать или максимизировать |k|. Из ограничения по y-координатам, |k| < b - 1 и 1 / |k| < b - 1. Тогда максимальное значение нашего выражения (b - 1) * ((b - 1) + 1 / (b - 1)) = (b - 1) ^ 2 + 1. Лемма доказана.

Нужно доказать, что при a > (b - 1) ^ 2 + 1 количество треугольников третьего типа не зависит от a. Это очевидно следует из леммы, ведь каждому такому треугольнику для a мы можем сопоставить треугольник для a + 1, полученный из первого сдвигом на 1 вправо. И каждому треугольнику 3 типа для a + 1 аналогично сопоставим треугольник 3 типа для a, сдвинув его на 1 влево.

C(a) — константа. Обозначим эту константу за c.

Итак, f(a, b) = f(a - 1, b) + (a - 1) * b * (b - 1) / 2 * 4 + c. Немного преобразований, и мы получаем формулу для f(a, b) через f((b - 1) ^ 2 + 1, b).

Преобразования

Реализация

ll fast(int a, int b)
{
    ll ans = 0;
    for (int a1=-a+1;a1<=a-1;a1++)
	for (int b1=-b+1;b1<=b-1;b1++)
	{
       	    if (a1 == 0 && b1 == 0) continue; 
	    for (int a2=-a+1;a2<=a-1;a2++)
	        for (int b2=-b+1;b2<=b-1;b2++)
		{
		    if (a2 == 0 && b2 == 0) continue;
		    if (b1 * b2 + a1 * a2 == 0 && a1 * b2 - b1 * a2 < 0)
		    {
		        int cnta = a - max(max(abs(a1), abs(a2)), abs(a1 - a2));
			int cntb = b - max(max(abs(b1), abs(b2)), abs(b1 - b2));
			if (cnta > 0 && cntb > 0) ans += cnta * cntb;
		    }
	        }
	}
    return ans;
}
struct polynom
{
    ll x0 = 0, x1 = 0, x2 = 0;
    void print()
    {
	cout << x2 << "x^2 + " << x1 << "x - " << -x0 << endl;
    }
    ld get(ld x)
    {
	return x2 * x * x + x1 * x + x0;
    }
};
ll get(int a, int b)
{
    if (a < b) swap(a, b);
    if (a <= (b - 1) * (b - 1) + 1) return fast(a, b);
    int x = fast((b - 1) * (b - 1) + 1, b);
    int y = fast((b - 1) * (b - 1) + 2, b);
    // y = x + c + (a - 1) * b * (b - 1) / 2 * 4;
    int c = y - x - ((b - 1) * (b - 1) + 1) * (b - 1) * b * 2;
    polynom P;
    P.x2 = b * b - b;
    P.x1 = c - b * b + b;
    P.x0 =-b*b*b*b*b*b + 5*b*b*b*b*b - 11*b*b*b*b + 13*b*b*b + b*b*(-8 - c) + b * (2 * c + 2) - 2 * c + x;
    return P.get(a);
}

К сожалению, c для разных b — разные, и я не смог найти между ними закономерность. Не помогли ни интерполяция, ни OEIS. Осталось несколько вещей, которые надо сделать:

Выразить c через b, ведь c зависит только от b
Решить задачу для a <= (b - 1) ^ 2 быстрее
Решить задачу для остроугольных треугольников

Будет жёстко.

UPD6: Можно ускорить решение до O(b^5), используя эту идею

Комментарии (14)

Показать архивные | Написать комментарий?

polosatic

14 месяцев назад, # |

Auto comment: topic has been translated by polosatic (original revision, translated revision, compare)

→ Ответить

bronze_coder

← Rev. 3 →

The right triangle problem is OEIS A077435

EDIT: OEIS A189814 gives the answer for rectangles.

14 месяцев назад, # ^ |

Thank you! I was quite sure that problem with right triangles can be solved in O(a * b) But unfortunately, f(n, n) also is not a polynomial of one variable.

OMG! I used too small ai for interpolation with constant b, so it didn't work. After using ai >= b ^ 2 everything works!

ANNIHILLATOR

Можно как минимум за квадрат решить, перебирая все пары направляющих векторов.

Действительно! Как я не догадался.

Автокомментарий: текст был обновлен пользователем polosatic (предыдущая версия, новая версия, сравнить).

kl1dd

Very nice

OIer1048576

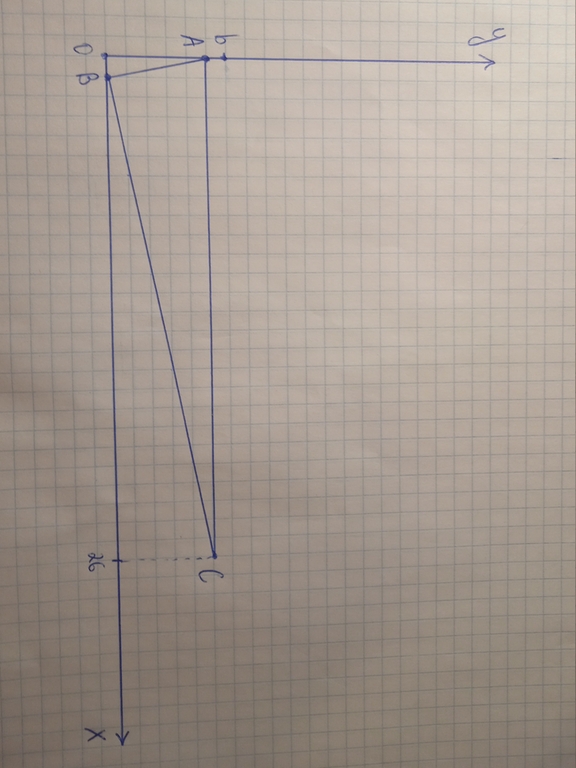
A not-implemented solution: let the triangle be tree vectors $$$a,b,c$$$.brute force $$$b-a$$$, and you will get $$$\dfrac{c-a}{|c-a|}$$$(which is rotate it for 90 deg(you can asumme ccw or cw))(In program, you can do it by a ). then you can brute force $$$c-a$$$ by $$$O(a + b)$$$. Then the problem is:

find how many triangles with vector $$$b-a=v$$$ and $$$c-a=w$$$?

which is trival.

If I understand you correctly, I have already implemented this solution in UPD3 of this blog

No. This solution is $$$O(ab(a+b))$$$.

UPD3 is Brute force b-a and c-a, find if b-a ⊥ c-a and find how many triangles with vector b-a and c-a.

But we can just brute force $$$|c-a|$$$(The length of c-a). the angle of $$$c-a$$$ is found by rotate $$$b-a$$$.

Wow! Good idea! Thank you.

why $$$O(a^2b^2(a+b))$$$ is $$$O(b^5)$$$? may $$$a \gg b^2$$$.

The solution in UPD5 needs to calculate

f((b - 1) ^ 2 + 1, b) and f((b - 1) ^ 2 + 2, b) to calculate f(a, b), it works in O(b ^ 6), but can be optimized to O(b ^ 5) using your method.

Блог пользователя polosatic

Попытки проинтерполировать

Что я хотел бы узнать:

Наконец-то нашёл формулу и решение за O(min(a, b) ^ 6)

Определения

Наконец-то нашёл формулу и решение за `O(min(a, b) ^ 6)`