diego_v1's blog

Data structure for amount of positive numbers in range [l,r]
By diego_v1, 10 years ago, In English

I've been trying to come up with an efficient data structure for the following problem for a couple of hours... without luck.

We have an array of numbers. Initially, all of them are 0. Then we have two types of operations...

  • update(l, r, v): Add v to all elements in the range [l, r]
  • query(l, r): Return the numbers of positive numbers in the range [l, r]

I thought about a segment tree where each node stores the minimum and maximum value found in that range, then in the query, if we are at a node where the minimum value is  > 0, we know that all numbers in the range are positive. But that data structure would visit every node in the tree in the worst case, so I was wondering if there's something more efficient.

Can anyone come up with a better idea?

  • Vote: I like it
  • +9
  • Vote: I do not like it

»
10 years ago, # |
  Vote: I like it 0 Vote: I do not like it

By the way, are there any data size limits specified for your problem?

→ Reply
»
10 years ago, # |
← Rev. 3   Vote: I like it 0 Vote: I do not like it

/*You can store in each node sorted segment [L, R] and variable "val", which is added to all elements in this node. Then you just binsearch for -val in the nodes. Memory NlogN. Each query log^2(N).*/

As Zlobober said, it's incorrect way.

→ Reply
  • »
    »
    10 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    It is impossible to recalculate the sorted order, for example, for the root node after each little update query. We do not know where exactly affected values are located in the sorted array, they could be mixed in some tricky way.

    → Reply
  • »
    »
    10 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    haha, because ur original answer was incorrect, u decided to strike /*comment*/ it? :D

    → Reply
»
10 years ago, # |
  Vote: I like it +16 Vote: I do not like it

I'm not sure if it is possible to implement such data structure using segment tree.

One can easily use sqrt-decomposition for this problem. Split the array into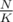 blocks of size K, and store integers in sorted order for every block. Update query will fully cover some blocks (for them just store additional shift value, i. e. the whole block should be decreased by 3), and no more than two blocks will be touched partially. For them you need to recalculate the whole block in O(K) time.

Using such structure it is easy to make queries on segments. Each query fully covers some blocks (we can answer for them using stored shift value and binary search), and touches max. 2 blocks partially, forcing us to answer in O(K) time.

So the total running time will be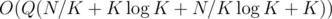 , that could be pretty small if you carefully choose appropriate K.

→ Reply
  • »
    »
    4 years ago, # ^ |
      Vote: I like it +3 Vote: I do not like it

    Very nice approach I just have a question, always the best value to choose for K is sqrt(N) or not?

    → Reply
    • »
      »
      »
      4 years ago, # ^ |
      ← Rev. 2   Vote: I like it +1 Vote: I do not like it

      You would generally want $$$K$$$ to be proportional to $$$\sqrt{N}$$$ so that the terms are all $$$\sqrt{N}$$$ or $$$\sqrt{N}\log{N}$$$, so the overall complexity is $$$O(Q\sqrt{N}\log{N})$$$.

      → Reply
»
10 years ago, # |
← Rev. 2   Vote: I like it 0 Vote: I do not like it

I came up with this idea when trying to solve the following problem: Given a collection of N rectangles in the plane, possibly overlapping, calculate the perimeter for all of them.

For that problem, I thought of a sweep plane algorithm and the data structure I mentioned in my post, only that in that case it's easier, because we only decrease ranges we previously increased, so with a couple of extra variables augmenting the tree, it's solved.

But then I thought about the more general case where we can update any range with any value, and I couldn't come up with a solution...

I think, just like Zlobober said, sqrt-decomposition is a nice solution if it can be solved offline.

→ Reply
»
10 years ago, # |
  Vote: I like it -12 Vote: I do not like it

i think ur problem is a bit similar to this one from Codechef (except that u allow v>0).
u can read the editorial here.

→ Reply
  • »
    »
    10 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    The fact that all updates have v < 0 changes everything. The solution for this problem does not apply to the general case I presented.

    → Reply
»
10 years ago, # |
← Rev. 4   Vote: I like it -13 Vote: I do not like it

I think it is possible to implement this operations using treap with lazy propagation. Lazy propagation should include two operations: "shift" of all values in subtree and "merge" "union" with other treap. I think it will be something like O(N(log N)^2). But it is possible I am wrong.

→ Reply
»
10 years ago, # |
← Rev. 5   Vote: I like it 0 Vote: I do not like it

Using Segment Tree, you could have each node the following way:

Node {
   vector<int> sorted_range;
   int delta;
}

All starting with delta = 0., then sorted range is the elements it represents, in a sorted way.

The space isn't really that much, on the i-th level, you will have N/2^i nodes with with (2^i)*N elements each. With logN levels it's NlogN space.

On the construction, if you are joining two nodes of x elements, you can just compare the first element of each (they are already sorted) and push the lowest to the new node, update the index, then keep doing it. Therefore, 2*x operations. Following the same logic as the space, it's also NlogN construction time.

Updates are just a matter of updating the delta, and would be in the usual O(logN) complexity with lazy propagation. Querying is the usual O(logN) + a binary search on the sorted array, so O(log²N).

It's kinda the same idea as Zlobober's sqrt decomposition, but on a segment tree. It would be asymptotically faster, although it uses a little more space. That being said, if the sqrt decomposition suits the problem, just go for it, cause the code for the segtree is way bigger :P

→ Reply
  • »
    »
    10 years ago, # ^ |
      Vote: I like it +8 Vote: I do not like it

    You can't perform an update in O(logN) on the tree with such structure.

    → Reply
  • »
    »
    10 years ago, # ^ |
      Vote: I like it +8 Vote: I do not like it

    The same solution was suggested in second answer to this post, although, it is wrong.

    Updates are not just a matter of updating deltas. You should also keep consistent all higher nodes. For example, you should keep the root node sorted. How can you rearrange its elements when you touch only some low-level elements that can be spread arbitraty across the sorted order of the root node?

    → Reply
»
10 years ago, # |
← Rev. 2   Vote: I like it 0 Vote: I do not like it

"Rule of thumb": When the question is "count numbers satisfying some inequalities", sqrt-decomposition is usually the right way.

Zlobober's solution is probably the best approach (in the sense that if there's a faster solution, it'd probably be very esotheric and since this isn't DS-heavy, it could work quite fast).

Also, sauce plz.

→ Reply
  • »
    »
    10 years ago, # ^ |
    ← Rev. 3   Vote: I like it 0 Vote: I do not like it

    What if we removed the update operation but we add a parameter to query operation X and count number of elements which is bigger than X, still the problem asks for "count numbers satisfying some inequalities" but a better approach than sqrt-decomposition exists.

    → Reply
    • »
      »
      »
      10 years ago, # ^ |
        Vote: I like it +11 Vote: I do not like it

      Do you know what a rule of thumb is?

      → Reply