LashaBukhnikashvili's blog

Math problem
By LashaBukhnikashvili, 10 years ago, In English

how prove that sqrt(2)+sqrt(3)+sqrt(5)+sqrt(7)+sqrt(11) is irrational number? thanks in advance

  • Vote: I like it
  • +31
  • Vote: I do not like it

»
10 years ago, # |
  Vote: I like it -25 Vote: I do not like it

i think supernatural is the best american tv series ever ! if you watch that you can get the solution of your prblem !In my opinion, you'd better consult the devils there. as i see, you are a smart man and you can succeed.

→ Reply
»
10 years ago, # |
← Rev. 2   Vote: I like it +15 Vote: I do not like it

You want to prove that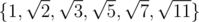 are linearly independent over the field of rational numbers. There should be a solution that uses algebraic manipulations but it will definitely be tedious. Good luck with that.

Nevertheless, this is a particular case of Iurie Boreico's(An exceptional IMO contestant) favourite problem. He gives a couple of difficult, but elementary proofs. Take a look if you are interested.

I have it bookmarked for over a year, hoping to sit and read it fully one day :'(

→ Reply
»
10 years ago, # |
  Vote: I like it +9 Vote: I do not like it

My favourite way to do this problem is the following.. http://qchu.wordpress.com/2009/07/02/square-roots-have-no-unexpected-linear-relationships/

Basically, first prove that if that number is rational, then it has to be an integer, and then find a prime for which all but one is a quadratic residue.(In this case 15401 works)

→ Reply
»
10 years ago, # |
  Vote: I like it +6 Vote: I do not like it

is an algebraic integer since it is the root of x2 - k = 0. The sum of two algebraic integers is itself an algebraic integer, so is an algebraic integer.

As such, if it is rational then it is also an integer. But take any semi-accurate approximation (to nearest tenth will do fine) and get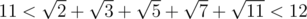 , so it is not an integer and thus not rational.

→ Reply
  • »
    »
    10 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    I am not getting one part. Why is it true that the minimal polynomial is monic? I assume you are using the rational root theorem after this to conclude that that expression is an integer, if it is rational.

    → Reply
    • »
      »
      »
      10 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      The definition of an algebraic integer is that there exists a monic polynomial with it as a root. So it just follows from the definition. And yes, the rational root theorem is the reason being rational implies being integral.

      (Of course I'm kind of cheating since the proof of two algebraic integers summing to another algebraic integer is basically equivalent to proving linear independency, but this is a nice quick intro into this kind of stuff)

      → Reply
      • »
        »
        »
        »
        10 years ago, # ^ |
          Vote: I like it 0 Vote: I do not like it

        Oh I see, I thought you were working with algebraic numbers. The proof that sum of two algebraic integers is another algebraic integer doesn't seem as easy as proving that for algebraic numbers(which just requires simple dimension arguments).

        But nice way to complete it, assuming this result :)

        → Reply