Hi CF ! Long time , no see. I have an interesting problem for you.
Statement
N dwarfs fell into a pit with depth of D cm. For every dwarf you know the height to the shoulders ( i.e. the distance from the ground to the shoulders ) and the arms length. The dwarfs try to escape from the pit , so they climb one on each other and get out of the pit.
Every dwarfs stands on the shoulders of other. If one dwarf reaches the top of the pit , he can get out of the pit. We denote the shoulder height of the i - th dwarf with hi and the arms length with li. A tower formed from k dwarfs j1, j2, ..., jk has the height hj1 + hj2 + ... + hjk . The dwarf hjk can get out of the pit if hj1 + hj2 + ... + hjk + ljk ≥ D. A tower can be formed in any possible way.
Your task is to determine how many dwarfs can get out of the pit. (1 ≤ N ≤ 2000)
Solution
Let's start with a simpler problem. Supose the length of the hands does not matter. ( i.e. jk - th dwarf can get out if hj1 + hj2 + ... + hjk ≥ D ) In this case we can sort the dwarfs decrasingly by hi and get out as many short dwarfs as possbile.
Note that a similar stategy would not work in our problem. An example would be N = 3 , D = 5 with ( h1 = 1 , l1 = 4 ) , ( h2 = 2 , l2 = 0 ) , ( h3 = 2 , l3 = 0 ).
With the previous strategy we would have the tower 2, 3, 1 and the dwarf 1 would be saved. But if the tower is 3, 1, 2 both 1 and 2 dwarfs can be saved.
We can conclude that a small dwarf with long hands can be placed closer to the base of the tower than other dwarfs. The order in wich the dwarfs will get out of the pit would rather be determined by the sum hi + li. Also we need not to forget that a heigher dwarf ( with hi bigger ) is more useful for the others than a small one.
Now , imagine we have already pulled out the optimum set of dwarfs. Let's now find how they came out. We can iterate through them and select the ones which we can put inside the hole and they still can get out. We will repeat that operation until all of them are in the hole.
From this reverse kind of thinking you got the idea that selecting a set of dwarfs who get out is a good one. We will sort the dwarfs decreasingly after hi ( in case of equalty after li ). If all the dwarfs from some set of dwarfs can get out we need to choose the last wich can get out , than he can be added to the tower.
We keep a vector in wich we will mark if some dwarf is in the set of the ones witch can get out. At each step we will try to add the dwarf with the maximum hi into the set.
for (int i=1;i<=N;++i)
{
int dwarf = oH[i]; // oH - order after height decreasingly
if ( good(dwarf) )
{
mark[ rev[dwarf] ] = 1; // put the dwarf in the set
// mark - the marking vector
// rev - the order in the original vector
h_init -= h[dwarf]; // h_init - the height of the tower
co++; // new dwarf added
}
else
mark[ rev[dwarf] ] = 0; // the dwarf is outside the set
}
Now we have to verify is we can add a dwarf in the set. For this we design a function wich says if a set of dwarfs is good or not. The last dwarf from the set wich will get out is the one with maximum hi + li. Then we can get it out of the set and repeat the process. Of course , we do not need sorting because we can precompute the vector oHL ( order after hi + li decreasingly ).
bool good(int dwarf)
{
int h_now = h_init - H[dwarf]; // h_now - acutal tower height
l[ rev[dwarf] ] = 1; // mark the dwarf
for (int i=N;i>=0;--i)
if ( l[i] == 1 )
{
if ( h_now + H[oHL[i]] + L[oHL[i]] >= D )
h_now += H[oHL[i]]; // if the dwarf can get out we put it in the tower
else
return 0; // else we have the guaranty that the actual set can't get out
}
return 1;
}
We verify in O(N) the introduction of some dwarf and we try to add every dwarf once. The final complexity is O(N2). Here is my source.
BONUS: The problem can be also solved by DP. Take a look. ;)










This problem was given at Russian Olympiad in Informatics in 2006.)
I can solve this problem in O(nlogn) by converting this problem to another.
Dual Problem is about deadlines, we have n tasks with deadline di, and takes ti minutes to complete the task. We need to complete maximum tasks.
so, Let's think that we complete tasks in order 1, 2, ... n, then for every i must hold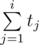 ≤ di.
≤ di.
In our problem, + li >= D.
+ li >= D.
Let's denote S as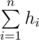
So it is the same task as deadline, with ti = hi, and di = li - D + S + hi.
And deadline task can be solved in O(nlogn) time.
Very nice solution. Thanks a lot !
This problem has NlogN version e-olimp
Sort all items by non-decreasing of hi + li.
Lest s — all dwarfs, which will get out. Initially s is empty. If the dwarf with the lowest hi + li can get out, let add it to s. Else, try to exchange it with the dwarf in s, whose hi is maximal possible.