RCC Qual 3 — Разбор задач

Задача А. Треугольники.

Идея: Андрей Станкевич.
Реализация: Анна Малова.
Разбор: Анна Малова.

В задаче требуется определить количество треугольников каждого типа, которые можно составить из четырех отрезков.

Переберем все возможные тройки отрезков. Из трех отрезков можно составить треугольник, если выполнено неравенство треугольника, то есть сумма любых двух сторон строго больше длины третьей стороны.

Рассмотрим отрезки a, b, c в порядке возрастания длины, тогда если выполнено равенство c² = a² + b², то треугольник является прямоугольным, если c² < a² + b² остроугольным, и если c² > a² + b²— тупоугольным

Задача B. Оригами.

Идея: Георгий Корнеев.
Реализация: Николай Ведерников.
Разбор: Николай Ведерников.

В задаче требуется проверить существует ли в прямоугольнике a на b подпрямоугольник площадью S, у которого стороны параллельны исходным.

Для этого переберём все такие x — делители числа S, и проверим, что x ≤ a и S ⁄ x ≤ b. Если существует хотя бы одна такая пара x и S ⁄ x, удолетворяющим ограничениям, то решение существует.

Время работы на один тестовый случай O(sqrt(S)).

Задача C. Митя и граф.

Идея: Жюри.
Реализация: Виталик Аксёнов.
Разбор: Виталик Аксёнов.

Первое наблюдение заключается в следующем: граф должен быть рёберным кактусом. Если он не получился таковым, то обязательно найдётся чётный цикл. Раз это кактус, то количество циклов равно m — (n — 1). А так как каждый цикл содержит в себе минимум 3 вершины, то 3·(m-(n — 1)) ≤ m. Отсюда получаем, что максимальное число рёбер равно 3·(n — 1) / 2.

При нечётных n, это мельница, то есть набор циклов длины 3, пересекающихся по 1 вершине, а при чётных n почти тоже самое, но еще одна висячая вершина соединена с любой другой ребром.

Задача D. Призы.

Идея: Виталик Аксёнов.
Реализация: Виталик Аксёнов.
Разбор: Виталик Аксёнов.

Мы знаем, что количества конфет, выданные участникам, должны убывать в зависимости от номера группы. Несложно убедиться, что любое удовлетворяющее разбиение конфет можно представить следующим способом:

В начале, в первой группе дети получают n конфет, во второй — n-1 конфет, ..., в последней — 1 конфету.
Далее мы можем прибавлять по одной конфете всем детям на префиксе групп. Это значит, что мы можем выбрать число p и увеличить a_i на единицу для любого i ≤ p.

Так как мы выбрали изначальное распределение, то из общего числа конфет можно сразу вычесть n·a₁+...+1·a_n. Несложно заметить, что операция распределения вычитает b_p = a₁+...+a_p. Итого, нам надо проверить, можем ли мы представить d в виде какой-то суммы b₁, ..., b_n, а это стандартная задача о рюкзаке.

Время работы O(nd).

Задача Е. Криптостойкие ключи

Идея: Виталий Демьянюк.
Реализация: Виталий Демьянюк.
Разбор: Виталий Демьянюк.

Дано множество чисел a₁, a₂, ..., a_n. Его замкнули относительно операций НОД и НОК. Требуется выяснить, принадлежит ли заданное число v замкнутому множеству S.

Представим v в виде p₁^q₁p₂^q₂... p_k^q_k, q_i > 0 , где p₁, p₂, ..., p_k — простые числа. Чтобы v принадлежало S необходимо чтобы для каждого i, 1 ≤ i ≤ k существовало j, 1 ≤ j ≤ n, такое что p_i^q_i ∣a_j и p_i^q_i+1 ∤a_j . Этот факт следует из того, что мы можем любое число представить в виде НОК(НОД(...), НОД(...), ..., НОД(...)), так как min(a, max(b, c)) = max(min(a, b), min(a, c)) и max(a, min(b, c)) = min(max(a, b), max(a, c)). Положим c_i равным наибольшему общему делителю чисел a_j, таких что p_i^q_i ∣a_j . Если все c_i делят v, то v принадлежит S. Оно может быть получено как наименьшее общее кратное всех c_i. В противном случае v не принадлежит S(это следует из свойств операций НОД и НОК).

Время работы O(nk + sqrt(v) ), где k — количество простых делителей числа v.

if angleA != 0 and angleB != 0 and angleC != 0: # не Существует if angleA < 90 and angleB < 90 and angleC < 90: # остроугольный if angleA == 90 or angleB == 90 or angleC == 90: # прямоугольный if angleA > 90 or angleB > 90 or angleC > 90: # тупоугольный

Комментарии (19)

Показать архивные | Написать комментарий?

ykalchevskiy

10 лет назад, # |

Небольшая опечатка:

При нечётных n, это мельница, то есть набор циклов длины 3, пересекающихся по 1 вершине, а при нечётных n почти тоже самое, но еще одна висячая вершина соединена с любой другой ребром.

→ Ответить

andrewzta

10 лет назад, # ^ |

Спасибо, исправил.

I_love_natalia

В этой фразе остро не хватает "например". И дать задачу потом посчитать, сколько таких конфигураций.

MaciejCzyzewski

Problem A. Triangles — альтернатива

Вы можете иметь простую функцию для расчета углов.

def angle (a, b, c):
    return math.degrees(math.acos((c**2 - b**2 - a**2)/(-2.0 * a * b)))

А потом проверить их с условиями.

← Rev. 2 →

И потом встретить тест, в котором acos(eps) == PI/2 — eps

BogolyubskiyAlexey

кстати таких тестов не было... что странно...

wackloner

+22

Если задача легко решается в целых числах, то любое вещественночисленное решение автоматом становится абсолютно ненужным хламом, уж прости, товарищ.

T-D-K

Мало того, что будут проблемы с точностью, как сказали выше. Если вывести такую формулу из теоремы косинусов: cos(angle) = (c^2-b^2-a^2)/(-2*a*b), а cos(angle)==0, если angle = 90, cos(angle)>0, если angle<90 и cos(angle) <0 если angle >90. Тогда можно просто рассчитывать косинус. Через cos = (c^2-b^2-a^2)/(-2*a*b), но тут можно заметить, что т.к. a и b всегда положительные, то просто можно считать r = (c^2-b^2-a^2), и сравнивать это с -cos, т.е. если r = 0 — треугольник прямоугольный, если r >0 — треугольник тупой, в остальных случаях острый. В итоге, получаем тоже решение что и в разборе.

marat.snowbear

В задаче D, уже перейдя ко второму уравнению, можно разделить его на один из коэффициентов (лучше всего на a₁, так как он минимальный) и решать уже в остатках от него. Тогда получается решение со сложностью O(na₁²), что при заданных ограничениях должно быть быстрее, чем O(nd). Вот код — 6709851, это пока самое быстрое решение к этой задаче в "тренировках".

Guliash

По поводу C объясните, пожалуйста, следующее:

Если два простых нечётных цикла пересекаются по как минимум одному ребру, то тогда существует чётный цикл. Это понятно. Но следует ли из этого существование простого чётного цикла?

Ac-93

Пусть у первого цикла длина l1, у второго l2, тогда сделаем цикл l1 + l2 — 2, где 2 это ребро по которому они пересекаются, его мы выкинем.

Это понятно. Что делать если пересечение не по одному ребру?

vlfom

Эм, ну если пересечение по k ребрам, то длина нового цикла будет l1+l2-2*k, ведь ребро встречается в обоих циклах, что тоже является четным числом.

Kaban-5

Мне кажется, что у такого способа (при нескольких рёбрах пересечения) есть небольшая проблема. Проблема в том, что может получиться сложный цикл (а не простой). На самом деле, может даже получиться несвязное объединение нечётных циклов.

Пример: циклы ABCDE и ABFCD. Получаем треугольники BFC и AED (если я правильно понял метод).

Назовём наши простые нечётные циклы L₁ и L₂.

Так как они имеют общее ребро, то они пересекаются хотя бы по 2 вершинам. Эти вершины разбивают цикл L₂ на цепи, внутри которых нет вершин L₁, а концы являются вершинами из L₁. Рассмотрим одну такую цепь (если вершин всего две, то цепей две, если три, то три (и так далее)). Пусть её концы — А и B. Есть 2 варианта:

1) A и B не являются соседними в L₁ или подцепи AB. Тогда оба пути, соединяющие A и B в L₁, не пересекаются с AB (выбранная подцепь не может пересекать L₁ нигде, так как все вершины из неё (кроме A и B) не лежат в L₁, а ребро AB не присутствует либо в подцепи, либо в L₁ по предположению) и имеют разную чётность. Тогда один из них можно приклеить к нашей цепи и получить простой чётный цикл.

2) Они соседние в L₁ и L₂. Если это верно для любой выбранной подцепи (иначе проведём рассуждение из пункта 1), то любое ребро из L₂ лежит в L₁. Аналогично получаем, что любое ребро из L₁ лежит в L₂. Имеем L₁ = L₂, что не так.

Надеюсь, нигде не ошибся.

Да, это похоже на правду. Спасибо большое!!!

Gerald

Кто-нибудь знает, как просто объяснить факт: "Если все ci делят v, то v принадлежит S".

Буду очень признателен, если кто-нибудь объяснит, как придумать решение такой задачи. Я честно сидел выписывал формулы и не понимаю, как додуматься, что нужно взять ci именно такие, как описано. Может можно как-то интуитивно это понять.

fetetriste

+17

Могу попробовать (сразу на оба вопроса). Каждому числу сопоставим разложение по простым, как в разборе: [q₁, ..., q_k]. Операция НОД – это MIN по каждой координате , а НОК – это MAX. Заметим здесь же, что никакие значения q_i, отличные от тех, что получатся при разбивании исходных чисел, получить нельзя. Будем собирать наше требуемое v отдельно по каждой координате. Для координаты i нам нужно собрать из исходных a_j какое-нибудь число, у которого в этой координате ровно q_i, а в остальных как можно меньше. Потом сделаем НОК всех результатов для каждой координаты и получим то, что надо, если это вообще возможно.

Собирать из исходных будем жадно: возьмём все те, у которых нужная координата не меньше, чем наша (это в разборе называется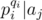 $\text{[math]}$ ), и сделаем им НОД, чтобы обрезать остальные координаты. "Если все c_i делят v, то v принадлежит S" как раз означает, что остальные коордианты обрезались достаточно хорошо, т.е. не превысили соответствующих q_j.

Если ещё доказать, что если таким способом нельзя получить v, то нельзя и никаким другим, то получается решение. В разборе на это намекает предложение о возможности перестановки MIN и MAX.

Да, достаточно понятно. Хорошее объяснение, спасибо. :)