Q. Given an array of N positive integers, find all pairs (ai, aj) such that Gcd(ai, aj) > 1.
1 ≤ N ≤ 105
How can this problem be solved?
| # | User | Rating |
|---|---|---|
| 1 | ecnerwala | 3648 |
| 2 | Benq | 3580 |
| 3 | orzdevinwang | 3570 |
| 4 | cnnfls_csy | 3569 |
| 5 | Geothermal | 3568 |
| 6 | tourist | 3565 |
| 7 | maroonrk | 3530 |
| 8 | Radewoosh | 3520 |
| 9 | Um_nik | 3481 |
| 10 | jiangly | 3467 |
| # | User | Contrib. |
|---|---|---|
| 1 | maomao90 | 174 |
| 2 | adamant | 164 |
| 2 | awoo | 164 |
| 4 | TheScrasse | 160 |
| 5 | nor | 159 |
| 6 | maroonrk | 156 |
| 7 | -is-this-fft- | 150 |
| 8 | SecondThread | 148 |
| 9 | pajenegod | 145 |
| 10 | BledDest | 144 |
Q. Given an array of N positive integers, find all pairs (ai, aj) such that Gcd(ai, aj) > 1.
1 ≤ N ≤ 105
How can this problem be solved?
| Name |
|---|



Where is this problem from?
http://www.hackerearth.com/problem/algorithm/gcd-recruit/
The link is not working.
Just look closer at the constraints :) It also can be solved for A[i] < = 106 .
Can you give another hint? I first thought precomputing euler totient function for all A[i] ≤ 3000 might be useful, but I dont think that will help.
I solved a similar problem on codechef a while ago, the key idea is to use inclusion-exclusion principle. If a number X is a multiple of Y, then X is also a multiple of all of Y's divisors. Now count for each number Y, the number of it's multiples that are present in your array and then apply inclusion-exclusion by making a loop from the highest Y to 1 and excluding every number's divisors.
The problem can be solved using mobius inversion formula but I don't understand it quite well but you can find pretty good tutorials about it on the internet!
Can you link me to the codechef problem ?
Here you go http://www.codechef.com/problems/COPRIME3
I contemplated over the idea but I am thinking that I need to know how many multiples of particular i <=10^6 are present in array how will that be processed efficiently! !please explain the process clearly !!
The problem constraints say that the largest number in the input will be less than 10^6 so here is what you can do. Put all number in a hash map with the frequency of each number.
Now say that you want to find how many multiples of 2 there are, you will go through the hash map and sum the counts of 2, 4, 6, 8, 10, 12, ...... 10^6
This will take time roughly equal to 10^6/2.
Now if you want to do the same thing for other numbers X from 3 to n, everyone will take (10^6/X) so the total time complexity would be 10^6/2 + 10^6/3 + 10^6/4 + 10^6/5 + ...... 10^6/n
This is equal to 10^6*(1/2 + 1/3 + 1/4 + 1/5 ..... + 1/n). The summation from 1/1 to 1/n is called harmonic series and is bounded by O (ln (n))
nlog(n) not always works if n is 1e6. It gives TLE (sometimes on cf and many times of CSES).
I bit of more explanations would be highly appreciated!
As there are atmost 8 distinct primes that a number can have a[i]<=10^6 , when we are at an index i we find how many of the numbers from 1 to i-1 have atleast one common divisor with the a[i] this can be done by PIE(PRINCIPLE OF INCLUSION AND EXCLUSION) ,we keep a global array G[] which tells us the number of elements which are divisible by the the index ,i.e G[i] = denotes number of elements uptill now which have i as one of it's divisors,to find no of elements from 1 to i-1 we use PIE and as our current number has atmost 8 distinct divisors say p1,p2,p3,...p8 then with PIE we can find total number of elements which are divisible by atleast one of the p1,p2,p3,...p8 ..we need G[p1 U p2 U p3 ...p8]= sigma G[pi] — sigma G[pi ^ pj] + sigma G[pi ^ pj ^pk] ......so on {^ =denotes intersection} time complexity of this step is 2^8 and after this step we will update G[] and increament at all positions where the a[i] is divisible similarly by generating 2^8 possible distinct prime combinations so overall time complexity = O(N*2^8).
upd: try this one this is based on modified PIE https://www.hackerearth.com/problem/algorithm/altered-primes/description/
can i get the code for this?
haha! searching for star values eh??
my algorithm for this problem went through about 2.7*10^7 operations. The basic idea was to have 2 for loops, one going from 1 to 3000 [say with variable i] and the other from 1 to 3000 [with variable j]. Then, if the gcd of the two is >0, and they are not the same, then you add X[i]*X[j] to one counter, where X[i] is the number of occurrences of integer i in the list provided. Else, if the gcd is > 0 and they are the same, then add X[i]*(X[i]-1)/2 to a separate counter. If we let the first counter be a and the second b, the answer is (a/2)+b
Note: This approach is much much easier then exclusion-inclusion principle.
ur idea is correct, but i think the answer should be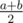 instead of
instead of 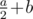 .
.
no it should be (a/2)+b, as we are not counting each pair b twice (for example, (2,2) is only counted once).
let a = [1, 2, 2, 3]. the correct answer for this case is 1 (only the pair (2, 2) is valid).
but according to ur method, x = [1, 2, 1]. this gives answer as 2, which is wrong.
Ohh I'm sorry... I mistyped when I put down my algorithm :P
It is fixed [it should be x[i]*(x[i]-1)/2]
They used the inclusion-exclusion principle to solve it when A[i]<=10^6
oh, makes sense.
Hello everyone, I came across a similar problem -- for a vector a, display number of unordered pairs such that GCD(a[i],a[j])>b such that i!=j. a[] and b are given in the input. Please help.
Where is this problem from?
// ~~~~~ include <bits/stdc++.h>
using namespace std;
define MAXN 1000001
define int long long
int spf[MAXN];
int M[MAXN] = { 0 };
void sieve()
{
}
void counthash(int x) { int temp; while (x != 1) { temp = spf[x]; if (x % temp == 0) { M[spf[x]]++; x = x / spf[x]; return; } while (x % temp == 0) x = x / temp; } }
void generate(int arr[], int n) { sieve(); for (int i = 0; i < n; i++) counthash(arr[i]);
}
set getF(int x) { set s; while (x != 1) { s.insert(spf[x]); x = x / spf[x]; } return s; }
int32_t main() { int n ; cin>>n;
}
~~~~~
//Here is the implementation.
how can we solve it for a[i] < 10^9 made a hash map for values present in array then used 2 loop as follows for(int i=2; i<1000000000; i++){ for(int j=i; j<1000000000; j+=i){ if(mp.find(j) != mp.end()){ cnt[i]++; } } } where cnt[i] counts multiple of i present in array by it's not working for 10^9.
Instead, let's calculate the no. of pairs i, j s.t. gcd(ai, aj) = 1 using mobius inversion and sqrt stuffs. Then we will know how to answer the original question. $$$S = \sum_{i = 1\cap i\subset A}^{N}\sum_{j = 1\cap j\subset A}^{N}[gcd(i, j) = 1] \newline = \sum_{i = 1\cap i\subset A}^{N}\sum_{j = 1\cap j\subset A}^{N}\sum_{d|gcd(i, j)}^{}\mu(d) \newline = \sum_{d = 1}^{N}\mu(d)(\sum_{i = 1\cap d\cdot i\subset A}^{N / d}1)^{2} \newline = \sum_{d = 1}^{N}\mu(d)\cdot (no. of\, multiples\, of\, d \subset A)^{2}$$$ Now we obeserve that each element of A has at most 10 divisors in (1e7, 1e9]. So for d <= 1e7 we loop to get 1st part of S where d <= 1e7 after precalculating no. of multiples of d in A and precalculating mobius values of all no.s upto 1e7. $$$\newline$$$ And to get 2nd part of S where d in (1e7, 1e9]: we create an array which contains all factors in (1e7, 1e9] of each element (these are ai / (10 smallest factors of ai)), then we can loop through the multiples of each element of this array and count how many of them are present. Also calculate mobius of each d present in this array. O(nsqrt(n) + 10*n*10^2). Actually, there can be at most 5 or 6 factors of ai in (1e7, 1e9] so I believe it would be possible to squeeze this within TL.