LashaBukhnikashvili's blog

One more Math problem

By LashaBukhnikashvili, 9 years ago, In English

I want to prove that for every 200 numbers,it can be choose 100 number which sum will divisible by 100.

I also thinks that,it will be correct: for every n numbers,we can choose x number which sum will divisible by x,if x<=n/2+n%2

can someone help me to prove them(of course,if 2th will be correct)? (sorry for my bad english)

  • Vote: I like it
  • +6
  • Vote: I do not like it

»
9 years ago, # |
  Vote: I like it 0 Vote: I do not like it

That's because all possible mods exist more than one time,i dont know the formal proof though

→ Reply
»
9 years ago, # |
← Rev. 2   Vote: I like it +11 Vote: I do not like it

First fact is right. Try searching for Erdős–Ginzburg–Ziv theorem (if there are 2n - 1 elements in multiset with elements from , there are n with zero sum).

→ Reply
»
9 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Suppose we have a sequence ai consisting of n integers. We can prove that for every nonnegative integer m <  = n we can choose at most m numbers from the sequence such that their sum is divisible by m.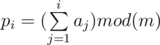
Let and p0 = 0
Take any m consecutive numbers from the sequence. According to pigeonhole principle, there will be at least two indexes L and R such that pL = pR. The sum of numbers with indexes from L + 1 to R will be divisible by m.

→ Reply
  • »
    »
    9 years ago, # ^ |
    ← Rev. 7   Vote: I like it +3 Vote: I do not like it

    We can prove that for every nonnegative integer m <  = n we can choose at most m numbers from the sequence such that their sum is divisible by m.

    Problem requries exactly 100 numbers, not less. So, it is Erdos-Ginzburgh-Ziv Theorem.

    → Reply